题目内容
设函数![]()
![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(Ⅱ)记函数![]() ,若函数
,若函数![]() 有零点,求
有零点,求![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,
时,![]() =
=![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]() =
=![]()
∵函数![]() 在
在![]() 上单调递增 ∴
上单调递增 ∴![]()
由![]() 得
得![]() 又
又![]()
![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .-----6分
.-----6分
(2)函数![]() 有零点即方程
有零点即方程![]() 有解
有解
即![]() 有解
有解
令![]() 当
当![]() 时
时![]()
∵![]()
∴函数![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]()
当![]() 时,
时,![]()
∵![]()
![]()
![]()
∴函数![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]()
∴方程![]() 有解时
有解时![]()
即函数![]() 有零点时
有零点时![]() -------12分
-------12分

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 .
. 时
时 取得极值,求a的值,并讨论
取得极值,求a的值,并讨论 .
.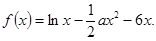
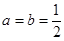 时,求函数
时,求函数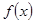 的单调区间;
的单调区间;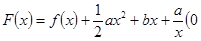 <
< ≤
≤ ,其图像上任意一点P
,其图像上任意一点P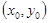 处切线的斜率
处切线的斜率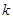 ≤
≤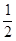 恒成立,求实数
恒成立,求实数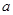 的取值范围;
的取值范围;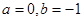 时,方程
时,方程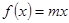 在区间
在区间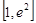 内有唯一实数解,求实数
内有唯一实数解,求实数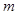 的取值范围。
的取值范围。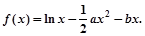
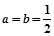 时,求
时,求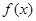 的最大值;
的最大值; ,(0
,(0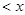 ≤3),其图象上任意一点
≤3),其图象上任意一点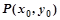 处切线的斜率
处切线的斜率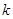 ≤
≤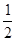 恒成立,求实数
恒成立,求实数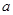 的取值范围;
的取值范围;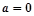 ,
,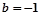 ,方程
,方程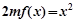 有唯一实数解,求正数
有唯一实数解,求正数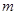 的值.
的值. .
.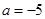 时,求函数
时,求函数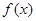 的定义域;
的定义域;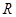 ,试求实数
,试求实数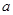 的取值范围.
的取值范围.