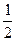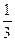题目内容
(本小题满分16分)
对于函数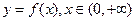 ,如果
,如果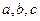 是一个三角形的三边长,那么
是一个三角形的三边长,那么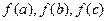 也是一个三角形的三边长,则称函数
也是一个三角形的三边长,则称函数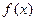 为“保三角形函数”.
为“保三角形函数”.
对于函数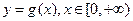 ,如果
,如果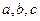 是任意的非负实数,都有
是任意的非负实数,都有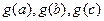 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数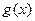 为“恒三角形函数”.
为“恒三角形函数”.
(Ⅰ)判断三个函数“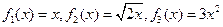 (定义域均为
(定义域均为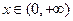 )”中,哪些是“保三角形函数”?请说明理由;
)”中,哪些是“保三角形函数”?请说明理由;
(Ⅱ)若函数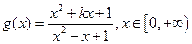 是“恒三角形函数”,试求实数
是“恒三角形函数”,试求实数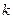 的取值范围;
的取值范围;
(Ⅲ)如果函数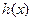 是定义在
是定义在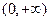 上的周期函数,且值域也为
上的周期函数,且值域也为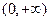 ,试证明:
,试证明: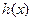 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
对于函数
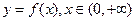 ,如果
,如果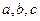 是一个三角形的三边长,那么
是一个三角形的三边长,那么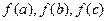 也是一个三角形的三边长,则称函数
也是一个三角形的三边长,则称函数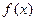 为“保三角形函数”.
为“保三角形函数”.对于函数
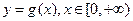 ,如果
,如果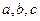 是任意的非负实数,都有
是任意的非负实数,都有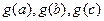 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数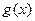 为“恒三角形函数”.
为“恒三角形函数”.(Ⅰ)判断三个函数“
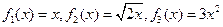 (定义域均为
(定义域均为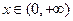 )”中,哪些是“保三角形函数”?请说明理由;
)”中,哪些是“保三角形函数”?请说明理由;(Ⅱ)若函数
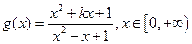 是“恒三角形函数”,试求实数
是“恒三角形函数”,试求实数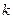 的取值范围;
的取值范围;(Ⅲ)如果函数
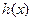 是定义在
是定义在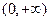 上的周期函数,且值域也为
上的周期函数,且值域也为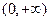 ,试证明:
,试证明: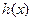 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.(Ⅰ)略
(Ⅱ)k的取值范围是
(Ⅲ)略
(Ⅱ)k的取值范围是

(Ⅲ)略
.解:(I)对于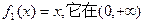 上是增函数,不妨设
上是增函数,不妨设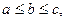
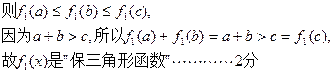
对于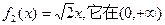 上是增函数,不妨设
上是增函数,不妨设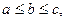
则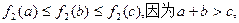
所以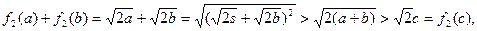
故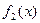 是“保三角形函数” ………………4
是“保三角形函数” ………………4 分
分
对于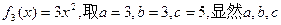 是一个三角形的三边长,
是一个三角形的三边长,
但因为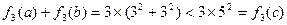 ,
,
所以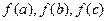 不是三角形的三边长,故
不是三角形的三边长,故
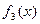 不是“保三角形函数” ………………6分
不是“保三角形函数” ………………6分
(II)法一: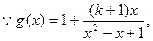
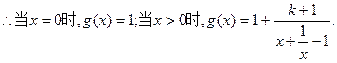
①当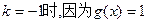 ,适量题意 ………………8分
,适量题意 ………………8分
②当
所以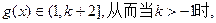
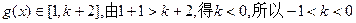 …………9分
…………9分
③当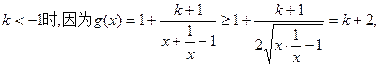
所以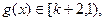
从而当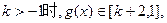
由
综上所述,所求k的取值范围是 ………………11分
………………11分
法二:
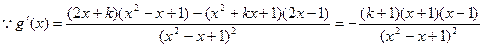 ,
,
①当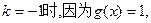 适合题意;
适合题意;
②当 上递增,在
上递增,在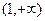 上递减,而
上递减,而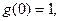
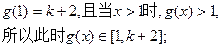
③当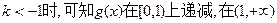 上递增,而
上递增,而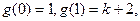
且当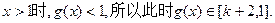
(以下同法一,按此方法求解的,类似给分)
(III)①因为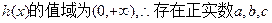
 ,
,
使得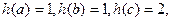 显然这样的
显然这样的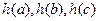 不是一个三角形的三边长,
不是一个三角形的三边长,
故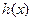 不是“恒三角形函数” ………………13分
不是“恒三角形函数” ………………13分
②因为 ,令
,令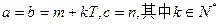 ,
,
且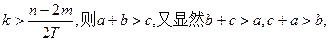
所以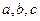 是一个三角形
是一个三角形 的三边长,但因为
的三边长,但因为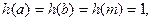
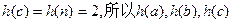 不是一个三角形的三边长,
不是一个三角形的三边长,
故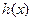
 也不是“保三角形函数” ………………16分
也不是“保三角形函数” ………………16分
(说明:也可以先证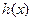 不是“保三角形函数”,然后据此知
不是“保三角形函数”,然后据此知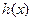 也不是“恒三角形函数”)
也不是“恒三角形函数”)
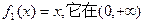 上是增函数,不妨设
上是增函数,不妨设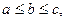
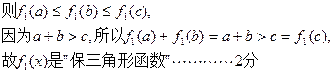
对于
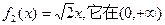 上是增函数,不妨设
上是增函数,不妨设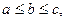
则
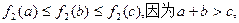
所以
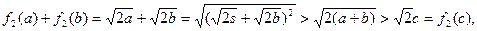
故
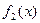 是“保三角形函数” ………………4
是“保三角形函数” ………………4 分
分对于
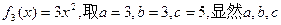 是一个三角形的三边长,
是一个三角形的三边长,但因为
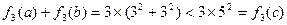 ,
,所以
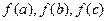 不是三角形的三边长,故
不是三角形的三边长,故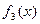 不是“保三角形函数” ………………6分
不是“保三角形函数” ………………6分(II)法一:
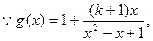
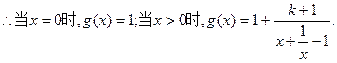
①当
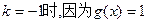 ,适量题意 ………………8分
,适量题意 ………………8分②当

所以
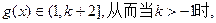
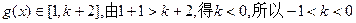 …………9分
…………9分③当
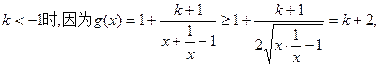
所以
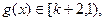
从而当
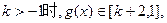
由

综上所述,所求k的取值范围是
 ………………11分
………………11分法二:
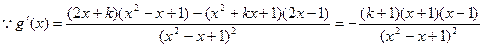 ,
,①当
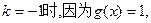 适合题意;
适合题意;②当
 上递增,在
上递增,在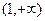 上递减,而
上递减,而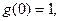
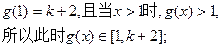
③当
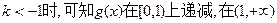 上递增,而
上递增,而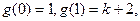
且当
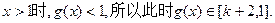
(以下同法一,按此方法求解的,类似给分)
(III)①因为
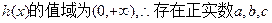
 ,
,使得
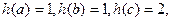 显然这样的
显然这样的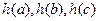 不是一个三角形的三边长,
不是一个三角形的三边长,故
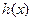 不是“恒三角形函数” ………………13分
不是“恒三角形函数” ………………13分②因为
 ,令
,令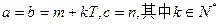 ,
,且
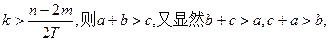
所以
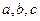 是一个三角形
是一个三角形 的三边长,但因为
的三边长,但因为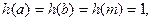
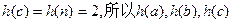 不是一个三角形的三边长,
不是一个三角形的三边长,故
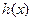
 也不是“保三角形函数” ………………16分
也不是“保三角形函数” ………………16分(说明:也可以先证
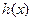 不是“保三角形函数”,然后据此知
不是“保三角形函数”,然后据此知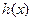 也不是“恒三角形函数”)
也不是“恒三角形函数”)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对任意的
对任意的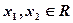 ,都有
,都有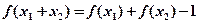 成
成 立,且当
立,且当 时,
时, 。
。 为奇函数;
为奇函数; 是R上的增函数;
是R上的增函数; ,解不等式
,解不等式 .
.



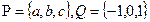 ,映射
,映射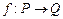 中满足
中满足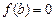 的映射个数是( )
的映射个数是( )
 ,
,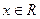 ,有下列4个命题:
,有下列4个命题: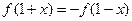 ,则
,则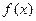 的图象自身关于点
的图象自身关于点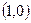 对称;
对称;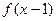 与
与 的图象关于直线
的图象关于直线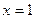 对称;
对称;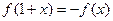 ,则
,则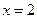 对称;
对称;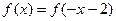 ,则
,则 ( )
( )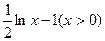
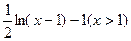
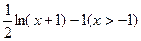
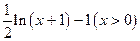
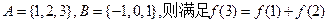 的映射
的映射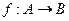 的个数是( )
的个数是( )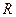 上的函数
上的函数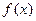 对任意实数
对任意实数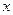 满足
满足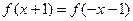 与
与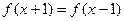 ,且当
,且当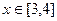 时,
时,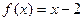 ,则 ( )
,则 ( )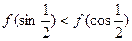

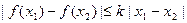 成立,则称函数
成立,则称函数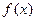 在定义域D上满足利普希茨条件。对于函数
在定义域D上满足利普希茨条件。对于函数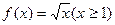 满足利普希茨条件,则常数k的最小值应是 ( )
满足利普希茨条件,则常数k的最小值应是 ( )