题目内容
对于椭圆
证明:椭圆![]() =1(a>b>0)的两焦点
=1(a>b>0)的两焦点
F1(-c,0)、F2(c,0),相应的准线方程分别是
x=![]() 2和x=
2和x=![]() .
.
∵椭圆上任一点到焦点的距离与它到相应准线的距离的比等于这个椭圆的离心率.
∴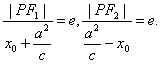
化简得:|PF1|=a+ex0,|PF2|=a-ex0.
温馨提示
|PF1|、|PF2|都是椭圆上的点到焦点的距离,习惯称作焦点半径.|PF1|=a+ex0,|PF2|=a-ex0称作焦半径公式,结合这两个公式,显然到焦点距离最远(近)点为长轴端点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 =1有KAM•KBM=-
=1有KAM•KBM=- .类似地,对于双曲线
.类似地,对于双曲线 -
- =1有KAM•KBM= .
=1有KAM•KBM= .
 =1有KAM•KBM=-
=1有KAM•KBM=- .类似地,对于双曲线
.类似地,对于双曲线 -
- =1有KAM•KBM= .
=1有KAM•KBM= .
 =1有KAM•KBM=-
=1有KAM•KBM=- .类似地,对于双曲线
.类似地,对于双曲线 -
- =1有KAM•KBM= .
=1有KAM•KBM= .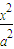
 =1有KAM•KBM=-
=1有KAM•KBM=-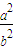 .类似地,对于双曲线
.类似地,对于双曲线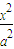 -
-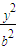 =1有KAM•KBM= .
=1有KAM•KBM= .