题目内容
若AB是过二次曲线中心的任一条弦,M是二次曲线上异于A、B的任一点,且AM、BM均与坐标轴不平行,则对于椭圆
 =1有KAM•KBM=-
=1有KAM•KBM=- .类似地,对于双曲线
.类似地,对于双曲线 -
- =1有KAM•KBM= .
=1有KAM•KBM= .
【答案】分析:设A,B所在直线为y=kx与椭圆方程联立设A(x1,y1)B(x2,y2)M(m,n)根据韦达定理表示出y1y2和x1x2,把点M的坐标代入椭圆方程,进而可表示出AM和BM的斜率,求得两斜率乘积的表达式,把y1+y2=0 x1+x2=0以及x1x2,y1y2,n2代入并整理就能得到答案.
解答:解:设A,B所在直线为y=kx与双曲线方程b2x2-a2y2=a2b2
联立得:(b2-a2k2)x2=a2b2
设A(x1,y1)B(x2,y2)M(m,n)
根据韦达定理
x1x2=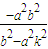 代入y=kx
代入y=kx
y1y2=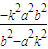
把M的坐标代入双曲线方程得n2=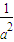 (a2b2+b2m2)
(a2b2+b2m2)
kAM•kBM=(y1-n)(y2-n)/(x1-m)(x2-m)
=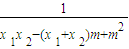 [y1y2-(y1+y2)n+n2]
[y1y2-(y1+y2)n+n2]
因为AB是过二次曲线中心的任一条弦,所以AB过原点
y1+y2=0 x1+x2=0
kAM•kBM=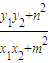
把x1x2,y1y2,n2代入并整理就能得到kAM•kBM=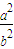
点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力.
解答:解:设A,B所在直线为y=kx与双曲线方程b2x2-a2y2=a2b2
联立得:(b2-a2k2)x2=a2b2
设A(x1,y1)B(x2,y2)M(m,n)
根据韦达定理
x1x2=
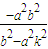 代入y=kx
代入y=kxy1y2=
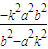
把M的坐标代入双曲线方程得n2=
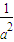 (a2b2+b2m2)
(a2b2+b2m2)kAM•kBM=(y1-n)(y2-n)/(x1-m)(x2-m)
=
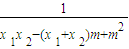 [y1y2-(y1+y2)n+n2]
[y1y2-(y1+y2)n+n2]因为AB是过二次曲线中心的任一条弦,所以AB过原点
y1+y2=0 x1+x2=0
kAM•kBM=
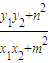
把x1x2,y1y2,n2代入并整理就能得到kAM•kBM=
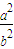
点评:本题主要考查了圆锥曲线的共同特征.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
 有
有 。类似地,对于双曲线
。类似地,对于双曲线 有
有 = 。
= 。 有
有 。类似地,对于双曲线
。类似地,对于双曲线 有
有 = 。
= 。 有
有 。类似地,对于双曲线
。类似地,对于双曲线 有
有 = 。
= 。
 =1有KAM•KBM=-
=1有KAM•KBM=- .类似地,对于双曲线
.类似地,对于双曲线 -
- =1有KAM•KBM= .
=1有KAM•KBM= .