题目内容
已知ABCD为正方形，点P为平面ABCD外一点，PD⊥AD，PD=AD=2，二面角P-AD-C为60°，则点C到平面PAB的距离为 ．
【答案】分析：想求点C到平面PAB的距离，先要求出棱锥P-BCD的体积，利用等积法，求出底面PAB的距离可得答案．
解答：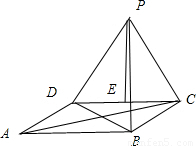
解：过P作PE⊥CD
∵ABCD为正方形，PD⊥AD，
∴∠PDC即为二面角P-AD-C为60°，
又∵PD=AD=2
∴PC=2，
则PE=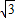
即为棱锥P-BCD的底面BCD上的高
∴棱锥P-BCD的V=
S△BCD•PE=
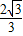
在△PBD中，PD=2，BD=2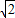
，PB=
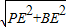=2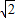
由海伦公式可得△PBD的面积S=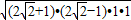
=
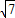
设点C到平面PAB的距离为d
则V=
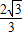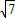Sd=
=
•
•d
解得d=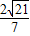
故答案为：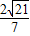
点评：本小题主要考查空间线面关系、二面角的度量、点线面距离的技计算等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力，要求同学们熟练掌握．
解答：
解：过P作PE⊥CD∵ABCD为正方形，PD⊥AD，
∴∠PDC即为二面角P-AD-C为60°，
又∵PD=AD=2
∴PC=2，
则PE=
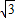即为棱锥P-BCD的底面BCD上的高∴棱锥P-BCD的V=
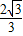
S△BCD•PE=在△PBD中，PD=2，BD=2
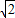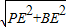，PB==2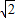由海伦公式可得△PBD的面积S=
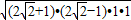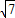
=设点C到平面PAB的距离为d
则V=
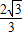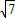Sd==••d解得d=
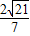
故答案为：
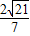
点评：本小题主要考查空间线面关系、二面角的度量、点线面距离的技计算等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力，要求同学们熟练掌握．
练习册系列答案
相关题目
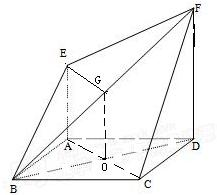如右图，已知ABCD为正方形，AE⊥平面ABCD，DF⊥平面ABCD，AD=DF=2AE=2．
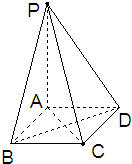如图，在四棱锥P-ABCD中，已知ABCD为正方形，且PA⊥平面ABCD，PA=2AB．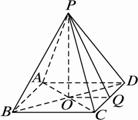
= 
+x
+y
；??
=x
+y
+
.?
，
，
.
平面
；