题目内容
已知抛物线
与直线
交于
，
两点．
（Ⅰ）求弦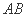
的长度；
（Ⅱ）若点
在抛物线
上，且
的面积为
，求点P的坐标．
(Ⅰ)设A（x1,y1)、B(x2,y2),
由
得x2-5x+4=0,Δ>0．
法一：又由韦达定理有x1+x2=5,x1x2=,
∴|AB|=
=
法二：解方程得： x=1或4，∴A、B两点的坐标为（1,-2)、（4,4）
∴|AB|=
(Ⅱ)设点
,设点P到AB的距离为d,则
,∴S△PAB=
·
·
=12，
∴
． ∴
，解得
或
∴P点为（9，6）或（4，-4）．
练习册系列答案
相关题目
表示的平面区域
的面积为
，则
( )
B． C．
D．
可以引圆
的两条切线，则实数
的取值范围是（ ）
B．
C．
D． 
中，
为方程
的两根，则
等于
，命题
，则
是
的 ( ) 
的最大值为 （ ）
上，并且与抛物线的准线及x轴都相切的圆的方程是（ ）
B．
D．
的展开式的常数项是