题目内容
函数y=log (4+3x-x2)
(4+3x-x2)
- A.有最大值无最小值
- B.有最小值无最大值
- C.既有最小值又有最大值
- D.既无最大值又无最小值
B
分析:令t=4+3x-x2,则由二次函数的性质可得函数t有最大值且没有最小者正值,故函数y=log (4+3x-x2)=
(4+3x-x2)= 有最小值而没有最大值,从而得出结论.
有最小值而没有最大值,从而得出结论.
解答:令t=4+3x-x2,则当x= 时,函数t有最大值为
时,函数t有最大值为  ,故函数y=log
,故函数y=log (4+3x-x2)=
(4+3x-x2)= 有最小值为
有最小值为 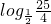 .
.
由于函数t不存在最小的正实数,故函数y=log (4+3x-x2)=
(4+3x-x2)= 没有大值,
没有大值,
故选B.
点评:题主要考查复合函数的单调性及最值,二次函数的性质,体现了转化的数学思想,属于中档题.
分析:令t=4+3x-x2,则由二次函数的性质可得函数t有最大值且没有最小者正值,故函数y=log
 (4+3x-x2)=
(4+3x-x2)= 有最小值而没有最大值,从而得出结论.
有最小值而没有最大值,从而得出结论.解答:令t=4+3x-x2,则当x=
 时,函数t有最大值为
时,函数t有最大值为  ,故函数y=log
,故函数y=log (4+3x-x2)=
(4+3x-x2)= 有最小值为
有最小值为 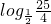 .
.由于函数t不存在最小的正实数,故函数y=log
 (4+3x-x2)=
(4+3x-x2)= 没有大值,
没有大值,故选B.
点评:题主要考查复合函数的单调性及最值,二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目