题目内容
【题目】已知抛物线方程![]() ,
,![]() 为焦点,
为焦点,![]() 为抛物线准线上一点,
为抛物线准线上一点,![]() 为线段
为线段![]() 与抛物线的交点,定义:
与抛物线的交点,定义:![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)证明:存在常数![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求得抛物线的焦点和准线方程,求得PF的斜率和方程,解得Q的坐标,由两点的距离公式可得所求值;
(2)求得P(﹣1,0),可得a=2,设P(﹣1,yP),yP>0,PF:x=my+1,代入抛物线方程,求得Q的纵坐标,计算2d(P)﹣|PF|,化简整理即可得证.
(1)抛物线方程y2=4x的焦点F(1,0),准线方程![]() ,当
,当![]() ,
,
kPF=![]() =
=![]() ,PF的方程为y=
,PF的方程为y=![]() (x﹣1),代入抛物线的方程,解得xQ=
(x﹣1),代入抛物线的方程,解得xQ=![]() ,
,
抛物线的准线方程为x=﹣1,可得|PF|=![]() =
=![]() ,
,
|QF|=![]() +1=
+1=![]() ,d(P)=
,d(P)=![]() =
=![]() ;
;
(2)当![]() 时,易得
时,易得![]() ,不妨设
,不妨设![]() ,
,![]()
直线![]() ,则
,则![]() ,
,
联立![]() ,得
,得![]() ,
, ![]()
![]() ,
,
![]()
![]()
![]() ,
,
所以存在常数![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目
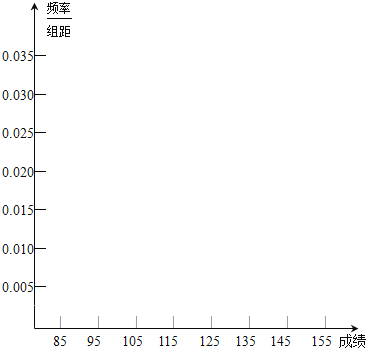
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.