题目内容
已知函数y=f(x),x∈N,f(x)∈N,满足:对任意x1,x2∈N,x1≠x2都有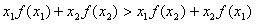 ;
;
(1)试证明:f(x)为N上的单调增函数;
(2) n∈N,且f(0)=1,求证:f(n)≥n+1;
n∈N,且f(0)=1,求证:f(n)≥n+1;
(3)对任意m,n∈N,有f(n+f(m))=f(n)+1, 证明: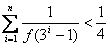 。
。
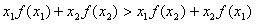 ;
;(1)试证明:f(x)为N上的单调增函数;
(2)
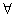 n∈N,且f(0)=1,求证:f(n)≥n+1;
n∈N,且f(0)=1,求证:f(n)≥n+1;(3)对任意m,n∈N,有f(n+f(m))=f(n)+1, 证明:
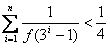 。
。 证明:(1)由 知,
知,
对任意 ,都有
,都有 ,
,
由于a-b<0,从而,所以函数f(x)为上的单调增函数。
(2) 由(1)可知, 都有f(n+1)>f(n),则有f(n+1)≥f(n)+1,
都有f(n+1)>f(n),则有f(n+1)≥f(n)+1,
∴f(n+1)-f(n)≥1,
∴f(n)-f(n-1)≥1,
…
∴f(2)-f(1)≥1,
∴f(1)-f(0)≥1,
由此可得f(n)-f(0)≥n,
∴f(n)≥n+1命题得证。
(3)令m=0,可得出f(0)=1,
又f(n+1)=f(n)+1,
则f(n)=n+1,
∴ 。
。
 知,
知,对任意
 ,都有
,都有 ,
,由于a-b<0,从而,所以函数f(x)为上的单调增函数。
(2) 由(1)可知,
 都有f(n+1)>f(n),则有f(n+1)≥f(n)+1,
都有f(n+1)>f(n),则有f(n+1)≥f(n)+1,∴f(n+1)-f(n)≥1,
∴f(n)-f(n-1)≥1,
…
∴f(2)-f(1)≥1,
∴f(1)-f(0)≥1,
由此可得f(n)-f(0)≥n,
∴f(n)≥n+1命题得证。
(3)令m=0,可得出f(0)=1,
又f(n+1)=f(n)+1,
则f(n)=n+1,
∴
 。
。
练习册系列答案
相关题目
已知函数y=f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |