Question

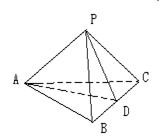
已知如图，P平面ABC，PA=PB=PC，∠APB=∠APC=60°，∠BPC=90 °求证：平面ABC⊥平面PBC

Answer 1

解析:

要证明面面垂直，只要在其呈平面内找一条线，然后证明直线与另一平面垂直即可。显然BC中点D，证明AD垂直平PBC即可

证明： 取BC中点D  连结AD、PD

         ∵PA=PB；∠APB=60°

         ∴ΔPAB为正三角形            

         同理ΔPAC为正三角形

         设PA=a

         在RTΔBPC中，PB=PC=a

         BC=a

         ∴PD=a

   在ΔABC中

   AD=

     =a

∵AD²+PD²=

        =a²=AP²

∴ΔAPD为直角三角形

即AD⊥DP

又∵AD⊥BC

∴AD⊥平面PBC

∴平面ABC⊥平面PBC