题目内容
(本小题满分l2分)(注意:在试题卷上作答无效)
(I)设函数 ,证明:当
,证明:当 时,
时,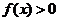 ;
;
(II)从编号1到100的100张卡片中每次随即抽取一张,然后放回,用这种方式连续抽取20次,设抽得的20个号码互不相同的概率为 .证明:
.证明: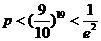
【答案】
【命题意图】本题为导数、概率与不等式的综合,主要考查导数的应用和利用导数证明不等式.考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
【解析】(I)  …………………………2分
…………………………2分
当 时,
时,  ,所以
,所以 为增函数,又
为增函数,又 ,因此当
,因此当 时,
时,
 .
…………………………5分
.
…………………………5分
(II)  .
.
又
所以 .
.
由(I)知: 当 时,
时, 
因此
 .
.
在上式中,令 ,则 19
,则 19 ,即
,即 .
.
所以 …………………………12分
…………………………12分
【点评】导数常作为高考的压轴题,对考生的能力要求非常高,它不仅要求考生牢固掌握基础知识、基本技能,还要求考生具有较强的分析能力和计算能力.估计以后对导数的考查力度不会减弱.作为压轴题,主要是涉及利用导数求最值解决恒成立问题,利用导数证明不等式等,有时还伴随对参数的讨论,这也是难点之所在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线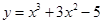 相切的直线方程.
相切的直线方程.