题目内容
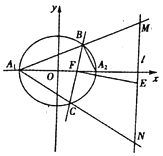
【题目】如图,已知椭圆![]()
![]() 的长轴
的长轴![]() ,长为4,过椭圆的右焦点
,长为4,过椭圆的右焦点![]() 作斜率为
作斜率为![]() (
(![]() )的直线交椭圆于
)的直线交椭圆于![]() 、
、![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 相交于
相交于![]() 、
、![]() 两点,设
两点,设![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由长轴长为4可得a,设出点B,C的坐标,利用斜率之积为![]() ,可得
,可得![]() ,即可得到b2,可得椭圆方程;
,即可得到b2,可得椭圆方程;
(2)设直线BC的方程为:y=k(x﹣1)与椭圆方程联立,得到根与系数的关系,直线![]() 的方程为:y
的方程为:y![]() (x+2)与x=4联立,可得点M,N的坐标,可得线段MN的中点E.利用根与系数的关系及其斜率计算公式可得
(x+2)与x=4联立,可得点M,N的坐标,可得线段MN的中点E.利用根与系数的关系及其斜率计算公式可得![]() ,只要证明
,只要证明![]() 1即可.
1即可.
(1)设![]() ,
,![]() ,因点
,因点![]() 在椭圆上,所以
在椭圆上,所以![]() ,
,
故![]() .又
.又![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]()
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() ,
,
联立方程组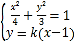 ,消去
,消去![]() 并整理得,
并整理得,
![]() ,则
,则![]() ,
,![]() .
.
直线![]() 的方程为
的方程为![]() ,令
,令![]() 得
得![]() ,
,
同理,![]() ;
;
所以![]() ,
,
代入化简得![]() ,即点
,即点![]() ,又
,又![]() ,
,
所以![]() ,所以
,所以![]() .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案【题目】某市《城市总体规划(![]() 年)》提出到
年)》提出到![]() 年实现“
年实现“![]() 分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身
分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身![]() 个方面构建“
个方面构建“![]() 分钟社区生活圈”指标体系,并依据“
分钟社区生活圈”指标体系,并依据“![]() 分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() )、良好小区(指数为
)、良好小区(指数为![]() )、中等小区(指数为
)、中等小区(指数为![]() )以及待改进小区(指数为
)以及待改进小区(指数为![]() )
)![]() 个等级.下面是三个小区
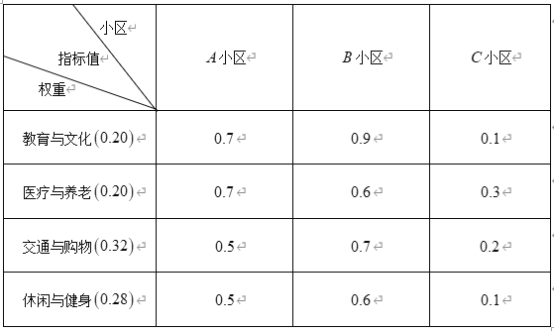
个等级.下面是三个小区![]() 个方面指标的调查数据:
个方面指标的调查数据:
注:每个小区“![]() 分钟社区生活圈”指数
分钟社区生活圈”指数![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值).
之间的一个数值).
现有![]() 个小区的“
个小区的“![]() 分钟社区生活圈”指数数据,整理得到如下频数分布表:
分钟社区生活圈”指数数据,整理得到如下频数分布表:
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)分别判断![]() 、
、![]() 、
、![]() 三个小区是否是优质小区,并说明理由;
三个小区是否是优质小区,并说明理由;
(Ⅱ)对这![]() 个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取
个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取![]() 个小区进行调查,若在抽取的
个小区进行调查,若在抽取的![]() 个小区中再随机地选取
个小区中再随机地选取![]() 个小区做深入调查,记这
个小区做深入调查,记这![]() 个小区中为优质小区的个数
个小区中为优质小区的个数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.