题目内容
已知数列![]() 满足:
满足: ![]() ,
,![]() (
(![]() 为正整数).
为正整数).
(1)令![]() ,求证:数列
,求证:数列![]() 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]()
(3) 比较![]() 与
与![]() 的大小,并证明之.
的大小,并证明之.
已知数列![]() 满足:
满足: ![]() ,
,![]() (
(![]() 为正整数).
为正整数).
(1)令![]() ,求证:数列
,求证:数列![]() 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]()
(3) 比较![]() 与
与![]() 的大小,并证明之.
的大小,并证明之.
【解】:(1)由![]() , 得:
, 得: ![]() ,
,
因![]()
![]() ,即当
,即当![]() 时,
时,![]() ,
,
又![]() ,
,![]() ,所以数列
,所以数列![]() 是首项和公差均为1的等差数列.
是首项和公差均为1的等差数列.
∴![]()
![]()
(2)由(Ⅰ)得,, ![]()
![]()
![]()
![]()
两式错位相减得到:
![]() ,
,![]()
(3)![]() ………(*)
………(*)
于是,确定![]() 与
与![]() 的大小关系等价于比较
的大小关系等价于比较![]() 与
与![]() 的大小,由
的大小,由![]()
![]() 可猜想当
可猜想当![]() 时,
时,![]() ,证明如下:
,证明如下:
证法1:(1)当![]() 时,由上验算显示成立。
时,由上验算显示成立。
(2)假设当![]() 时不等式成立,即
时不等式成立,即![]()
则当![]() 时,
时,![]()
所以,当![]() 时猜想也成立,综合(1)(2)可知,对一切
时猜想也成立,综合(1)(2)可知,对一切![]() 的正整数,都有
的正整数,都有![]()
综上所述,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
证法2:
![]()
![]()
综上所述,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于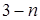 B.
B. C.
C.  D.
D. 
 满足:
满足: .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.