题目内容
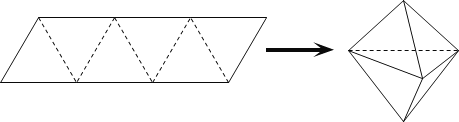
【题目】在四棱锥
中，底面
是正方形，顶点
在底面的射影是底面的中心，且各顶点都在同一球面上，若该四棱锥的侧棱长为
，体积为4，且四棱锥的高为整数，则此球的半径等于（ ）（参考公式：
）
A. 2B. 
C. 4D. 
【答案】B
【解析】
如图所示，设底面正方形
的中心为
，正四棱锥
的外接球的球心为
，半径为
.则在
中，有
，再根据体积为
可求
及
，在
中，有
，解出后可得正确的选项.
如图所示，设底面正方形的中心为，正四棱锥的外接球的球心为，半径为.
设底面正方形的边长为
，正四棱锥的高为
，则
.
因为该正四棱锥的侧棱长为
，所以
，即……①
又因为正四棱锥的体积为4，所以
……②
由①得
，代入②得
，配凑得
，
，即
，
得
或
.
因为
，所以，再将代入①中，解得，
所以
，所以
.
在
中，由勾股定理，得
，
即，解得
，所以此球的半径等于
.故选B.
练习册系列答案
相关题目
