题目内容
画出函数y=2|x+1|的图象,并根据图象指出它的单调区间.
解:去掉绝对值号把函数表示为分段函数:
y=2|x+1|=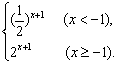
其图象分成两部分,一部分是将y1=(![]() )x+1(x<-1)的图象作出,而它的图象可以看作将y=(
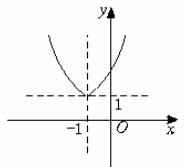
)x+1(x<-1)的图象作出,而它的图象可以看作将y=(![]() )x的图象沿x轴的负方向平移一个单位而得到,另一部分是将y=2x+1(x≥-1)的图象作出,而它的图象可以看作将y=2x的图象沿x轴的负方向平移一个单位而得到.如下图,由图知,单调递减区间是(-∞,-1),单调递增区间是[-1,+∞].
)x的图象沿x轴的负方向平移一个单位而得到,另一部分是将y=2x+1(x≥-1)的图象作出,而它的图象可以看作将y=2x的图象沿x轴的负方向平移一个单位而得到.如下图,由图知,单调递减区间是(-∞,-1),单调递增区间是[-1,+∞].
点评:作函数图象首先要化简函数解析式y=2![]() =
=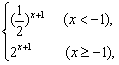 然后与熟悉函数的图象建立联系,根据图象的性质(函数的性质),利用图象的平移变换及对称变换,达到 目的.
然后与熟悉函数的图象建立联系,根据图象的性质(函数的性质),利用图象的平移变换及对称变换,达到 目的.

练习册系列答案
相关题目