题目内容
函数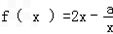 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(Ⅰ)当a=﹣1时,求函数y=f(x)的值域;
(Ⅱ)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(Ⅲ)求函数y=f(x)在x∈(0,1]上的最大值及最小值,并求出函数取最值时x的值
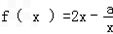 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).(Ⅰ)当a=﹣1时,求函数y=f(x)的值域;
(Ⅱ)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(Ⅲ)求函数y=f(x)在x∈(0,1]上的最大值及最小值,并求出函数取最值时x的值
解:(Ⅰ)显然函数y=f(x)的值域为 ;
;
(Ⅱ)∵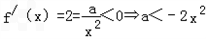 在定义域上恒成立
在定义域上恒成立
而﹣2x2∈(﹣2,0)∴a≤﹣2
(Ⅲ)当a≥0时,函数y=f(x)在(0.1]上单调增,无最小值,
当x=1时取得最大值2﹣a;
由(2)得当a≤﹣2时,函数y=f(x)在(0.1]上单调减,无最大值,
当x=1时取得最小值2﹣a;
当﹣2<a<0时,函数y=f(x)在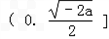 上单调减,
上单调减,
在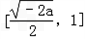 上单调增,无最大值,
上单调增,无最大值,
当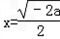 时取得最小值
时取得最小值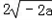 .
.
 ;
;(Ⅱ)∵
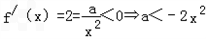 在定义域上恒成立
在定义域上恒成立而﹣2x2∈(﹣2,0)∴a≤﹣2
(Ⅲ)当a≥0时,函数y=f(x)在(0.1]上单调增,无最小值,
当x=1时取得最大值2﹣a;
由(2)得当a≤﹣2时,函数y=f(x)在(0.1]上单调减,无最大值,
当x=1时取得最小值2﹣a;
当﹣2<a<0时,函数y=f(x)在
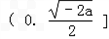 上单调减,
上单调减,在
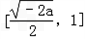 上单调增,无最大值,
上单调增,无最大值,当
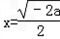 时取得最小值
时取得最小值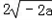 .
.
练习册系列答案
相关题目
 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数). 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数). 的定义域为(0,2),则函数
的定义域为(0,2),则函数 的定义域是
的定义域是