Question

已知函数f（x）=x﹣4+，x∈（0，4），当x=a时，f（x）取得最小值b，则在直角坐标系中函数g（x）=的图象为（　　）

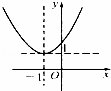
A．

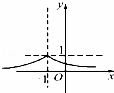
B．

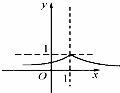
C．

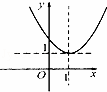
D．

Answer 1

考点：

指数型复合函数的性质及应用；函数的图象．

专题：

计算题；作图题．

分析：

由f（x）=x﹣4+=x+1+，利用基本不等式可求f（x）的最小值及最小值时的条件，可求a，b，可得g（x）==，结合指数函数的性质及函数的图象的平移可求

解答：

解：∵x∈（0，4），

∴x+1＞1

∴f（x）=x﹣4+=x+1+=1

当且仅当x+1=即x=2时取等号，此时函数有最小值1

∴a=2，b=1，

此时g（x）==，

此函数可以看着函数y=的图象向左平移1个单位

结合指数函数的图象及选项可知B正确

故选B

点评：

本题主要考察了基本不等式在求解函数的最值中的应用，指数函数的图象及函数的平移的应用是解答本题的关键