题目内容
函数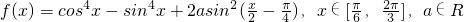
(1)当a=-4时,求函数f(x)的最大值;
(2)设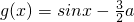 ,且f(x)≤-ag(x)在
,且f(x)≤-ag(x)在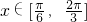 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
解:(1)∵a=-4
∴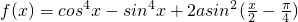
=cos2x-4(1-cos(x- ))
))
=1-2sin2x+4sinx-4
=-2(sinx-1)2-1,
∵x∈[ ,
, ],
],
∴ ≤sinx≤1,当sinx=1时,f(x)取得最大值-1,
≤sinx≤1,当sinx=1时,f(x)取得最大值-1,
∴函数f(x)的最大值为-1;
(2)∵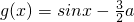 ,且f(x)≤-ag(x)在
,且f(x)≤-ag(x)在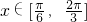 上恒成立,
上恒成立,
∴-a(sinx- a)≥f(x)=cos2x+a[1-sinx]在
a)≥f(x)=cos2x+a[1-sinx]在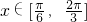 上恒成立,
上恒成立,
即 a2-a≥cos2x,x∈[
a2-a≥cos2x,x∈[ ,
, ]恒成立,
]恒成立,
而x∈[ ,
, ]时,(cos2x)max=cos
]时,(cos2x)max=cos =
= ,
,
∴即 a2-a≥
a2-a≥ ,
,
∴a≥1或a≤- .
.
实数a的取值范围为(-∞,- ]∪[1,+∞).
]∪[1,+∞).
分析:(1)当a=-4时,利用三角函数公式可将f(x)化为:f(x)=-2(sinx-1)2-1,x∈[ ,
, ],从而可求函数f(x)的最大值;
],从而可求函数f(x)的最大值;
(2)由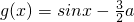 ,且f(x)≤-ag(x)可得
,且f(x)≤-ag(x)可得 a2-a≥cos2x,x∈[
a2-a≥cos2x,x∈[ ,
, ]恒成立,从而可求得实数a的取值范围.
]恒成立,从而可求得实数a的取值范围.
点评:本题考查三角函数的化简求值,难点在于(2)含参数的条件的转化与应用,突出考查三角函数公式的综合运用与恒成立问题,属于难题.
∴
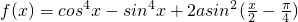
=cos2x-4(1-cos(x-
 ))
))=1-2sin2x+4sinx-4
=-2(sinx-1)2-1,
∵x∈[
 ,
, ],
],∴
 ≤sinx≤1,当sinx=1时,f(x)取得最大值-1,
≤sinx≤1,当sinx=1时,f(x)取得最大值-1,∴函数f(x)的最大值为-1;
(2)∵
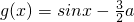 ,且f(x)≤-ag(x)在
,且f(x)≤-ag(x)在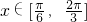 上恒成立,
上恒成立,∴-a(sinx-
 a)≥f(x)=cos2x+a[1-sinx]在
a)≥f(x)=cos2x+a[1-sinx]在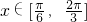 上恒成立,
上恒成立,即
 a2-a≥cos2x,x∈[
a2-a≥cos2x,x∈[ ,
, ]恒成立,
]恒成立,而x∈[
 ,
, ]时,(cos2x)max=cos
]时,(cos2x)max=cos =
= ,
,∴即
 a2-a≥
a2-a≥ ,
,∴a≥1或a≤-
 .
.实数a的取值范围为(-∞,-
 ]∪[1,+∞).
]∪[1,+∞).分析:(1)当a=-4时,利用三角函数公式可将f(x)化为:f(x)=-2(sinx-1)2-1,x∈[
 ,
, ],从而可求函数f(x)的最大值;
],从而可求函数f(x)的最大值;(2)由
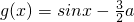 ,且f(x)≤-ag(x)可得
,且f(x)≤-ag(x)可得 a2-a≥cos2x,x∈[
a2-a≥cos2x,x∈[ ,
, ]恒成立,从而可求得实数a的取值范围.
]恒成立,从而可求得实数a的取值范围.点评:本题考查三角函数的化简求值,难点在于(2)含参数的条件的转化与应用,突出考查三角函数公式的综合运用与恒成立问题,属于难题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 已知函数f(x)=|x|•(a-x),a∈R.
已知函数f(x)=|x|•(a-x),a∈R.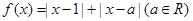
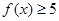 的解集
的解集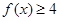 对
对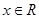 恒成立,求a的取值范围。
恒成立,求a的取值范围。