题目内容
若f(x)=4x,则f-1(4x)=| 1 |
| 2 |
| 10 |
分析:(1)本题可由原函数f(x)的解析式先求出反函数f-1(x)的解析式,最后将自变量取值4x代入反函数f-1(x)的解析式,结合对数函数运算性质可得答案,
(2)由自变量求解函数值可得x与a的等式,进而用自变量x表示a后代入函数解析式,从而可得仅含变量x的方程,由此解出x的值.
(2)由自变量求解函数值可得x与a的等式,进而用自变量x表示a后代入函数解析式,从而可得仅含变量x的方程,由此解出x的值.
解答:(1)由f(x)=4x得f-1(x)=log4x,所以f-1(4x)=log44x=x,
故答案为x
(2)令x=lga得 a=10x所以f(lga)=f(x)=(10x)x-
=10x2-
=
=10
,故x2-
x=
解得x=1或-
,代入a=10x,所以a=10或10-
故答案为10或10-
故答案为x
(2)令x=lga得 a=10x所以f(lga)=f(x)=(10x)x-
| 1 |
| 2 |
| x |
| 2 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为10或10-
| 1 |
| 2 |
点评:第一小题主要考查反函数知识和对数函数的运算性质,是对基础知识的考查,第二小题在考查函数值的基础之上,主要考查对数与指数之间的互化,以及指数幂运算性质,其中包括对解一元二次方程等基础的考查,难度较大.

练习册系列答案
相关题目
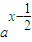 ,且f(lga)=
,且f(lga)=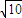 ,则a= .
,则a= .