题目内容
已知向量,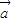 =(m,1),
=(m,1),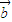 =(sinx,cosx),f(x)=
=(sinx,cosx),f(x)=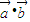 且满足f(
且满足f(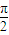 )=1.
)=1.(1)求函数y=f(x)的解析式;并求函数y=f(x)的最小正周期和最值及其对应的x值;
(2)锐角△ABC中,若f(
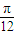 )=
)=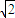 sinA,且AB=2,AC=3,求BC的长.
sinA,且AB=2,AC=3,求BC的长.
【答案】分析:(1)根据向量数量积的坐标运算公式,得f(x)=msinx+cosx,从而由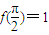 解出m=1.因此f(x)=sinx+cosx,化简得
解出m=1.因此f(x)=sinx+cosx,化简得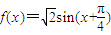 ,再结合正弦函数的图象与性质,即可得到函数的最小正周期和最值及其对应的x值;
,再结合正弦函数的图象与性质,即可得到函数的最小正周期和最值及其对应的x值;
(2)由(1)中的表达式,根据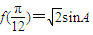 及△ABC是锐角三角形解出A=
及△ABC是锐角三角形解出A=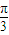 ,再利用余弦定理即可解出BC的长.
,再利用余弦定理即可解出BC的长.
解答:解:(1)∵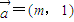 ,
,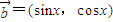 ,
,
∴f(x)=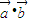 =msinx+cosx,
=msinx+cosx,
又∵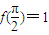 ,∴
,∴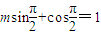 解之得m=1.…(2分)
解之得m=1.…(2分)
∴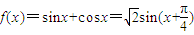 .…(4分)
.…(4分)
可得函数的最小正周期T=2π.…(5分)
当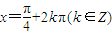 时,f(x)的最大值为
时,f(x)的最大值为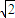 ;当
;当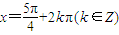 时,f(x)最小值为
时,f(x)最小值为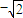 ….(7分)
….(7分)
(2)∵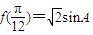 ,可得
,可得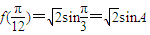
∴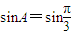 .…(8分)
.…(8分)
∵A是锐角△ABC的内角,∴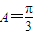 .…(9分)
.…(9分)
∵AB=2,AC=3
∴由余弦定理得:BC2=AC2+AB2-2•AB•ACcosA=7.…(10分)
解之得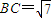 (舍负).…(12分)
(舍负).…(12分)
点评:本题给出向量含有三角函数式的坐标形式,求函数f(x)=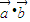 的表达式,并依此求解三角形ABC的边BC长,着重考查了向量数量积公式、三角函数的图象与性质和余弦定理等知识,属于中档题.
的表达式,并依此求解三角形ABC的边BC长,着重考查了向量数量积公式、三角函数的图象与性质和余弦定理等知识,属于中档题.
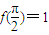 解出m=1.因此f(x)=sinx+cosx,化简得
解出m=1.因此f(x)=sinx+cosx,化简得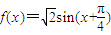 ,再结合正弦函数的图象与性质,即可得到函数的最小正周期和最值及其对应的x值;
,再结合正弦函数的图象与性质,即可得到函数的最小正周期和最值及其对应的x值;(2)由(1)中的表达式,根据
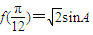 及△ABC是锐角三角形解出A=
及△ABC是锐角三角形解出A=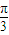 ,再利用余弦定理即可解出BC的长.
,再利用余弦定理即可解出BC的长.解答:解:(1)∵
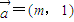 ,
,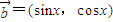 ,
,∴f(x)=
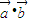 =msinx+cosx,
=msinx+cosx,又∵
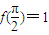 ,∴
,∴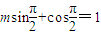 解之得m=1.…(2分)
解之得m=1.…(2分)∴
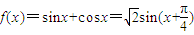 .…(4分)
.…(4分)可得函数的最小正周期T=2π.…(5分)
当
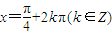 时,f(x)的最大值为
时,f(x)的最大值为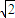 ;当
;当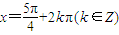 时,f(x)最小值为
时,f(x)最小值为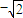 ….(7分)
….(7分)(2)∵
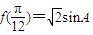 ,可得
,可得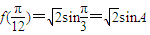
∴
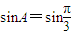 .…(8分)
.…(8分)∵A是锐角△ABC的内角,∴
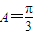 .…(9分)
.…(9分)∵AB=2,AC=3
∴由余弦定理得:BC2=AC2+AB2-2•AB•ACcosA=7.…(10分)
解之得
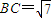 (舍负).…(12分)
(舍负).…(12分)点评:本题给出向量含有三角函数式的坐标形式,求函数f(x)=
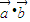 的表达式,并依此求解三角形ABC的边BC长,着重考查了向量数量积公式、三角函数的图象与性质和余弦定理等知识,属于中档题.
的表达式,并依此求解三角形ABC的边BC长,着重考查了向量数量积公式、三角函数的图象与性质和余弦定理等知识,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目