Question

【题目】有编号为1，2，3…n的n个学生，入座编号为1，2，3…n的n个座位，每个学生规定坐一个座位, 设学生所坐的座位号与该生的编号不同的学生人数为, 已知时, 共有6种坐法.

（1）求的值；

（2）求随机变量的概率分布列及数学期望．

Answer 1

【答案】（1）；（2）分布列详见解析，.

【解析】

试题（1）解题的关键是ξ=2时，共有6种坐法，写出关于n的表示式，解出未知量，把不合题意的舍去．

（2）学生所坐的座位号与该生的编号不同的学生人数为ξ，由题意知ξ的可能取值是0，2，3，4，当变量是0时表示学生所坐的座位号与该生的编号都相同，当变量是2时表示学生所坐的座位号与该生的编号有2个相同，理解变量对应的事件，写出分布列和期望．

解：（1）∵当ξ=2时，有Cn2种坐法，

∴Cn2=6，

即，

n2﹣n﹣12=0，n=4或n=﹣3（舍去），

∴n=4．

（2）∵学生所坐的座位号与该生的编号不同的学生人数为ξ，

由题意知ξ的可能取值是0，2，3，4，

当变量是0时表示学生所坐的座位号与该生的编号都相同，

当变量是2时表示学生所坐的座位号与该生的编号有2个相同，

当变量是3时表示学生所坐的座位号与该生的编号有1个相同，

当变量是4时表示学生所坐的座位号与该生的编号有0个相同，

∴，

，

，

，

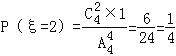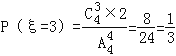∴ξ的概率分布列为：

ξ	0	2	3	4
P

∴．