题目内容
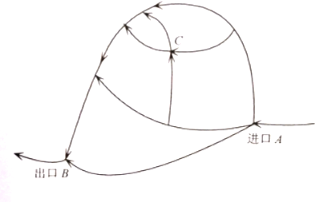
【题目】如图,已知城市![]() 周边有两个小镇
周边有两个小镇![]() 、
、![]() ,其中乡镇
,其中乡镇![]() 位于城市
位于城市![]() 的正东方
的正东方![]() 处,乡镇
处,乡镇![]() 与城市
与城市![]() 相距
相距![]() ,
,![]() 与
与![]() 夹角的正切值为2,为方便交通,现准备建设一条经过城市
夹角的正切值为2,为方便交通,现准备建设一条经过城市![]() 的公路
的公路![]() ,使乡镇
,使乡镇![]() 和
和![]() 分别位于
分别位于![]() 的两侧,过
的两侧,过![]() 和
和![]() 建设两条垂直
建设两条垂直![]() 的公路
的公路![]() 和
和![]() ,分别与公路
,分别与公路![]() 交汇于
交汇于![]() 、
、![]() 两点,以
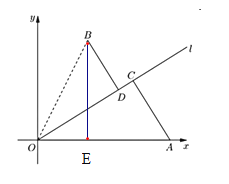
两点,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的平面直角坐标系
轴,建立如图所示的平面直角坐标系![]() .
.

(1)当两个交汇点![]() 、
、![]() 重合,试确定此时
重合,试确定此时![]() 路段长度;
路段长度;
(2)当![]() ,计算此时两个交汇点
,计算此时两个交汇点![]() 、
、![]() 到城市
到城市![]() 的距离之比;
的距离之比;
(3)若要求两个交汇点![]() 、
、![]() 的距离不超过
的距离不超过![]() ,求
,求![]() 正切值的取值范围.
正切值的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)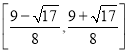 .
.
【解析】
(1)先求出直线![]() 的斜率为1,点B的坐标为
的斜率为1,点B的坐标为![]() ,再利用点到直线的距离为|BD|=
,再利用点到直线的距离为|BD|=![]() ;(2)设直线AB的斜率为
;(2)设直线AB的斜率为![]() ,先求出
,先求出![]() 再求出
再求出![]() ,即得
,即得![]() ;(3)先求出
;(3)先求出![]() ,再求出
,再求出![]() 解不等式即得解.
解不等式即得解.
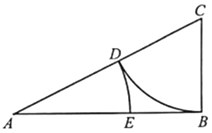
(1)当两个交汇点![]() 、
、![]() 重合时,则AC,BD公路共线,
重合时,则AC,BD公路共线,
过点B作BE⊥AO,垂足为E, 则![]() ,
,
所以AE=![]() ,所以|BE|=|AE|,
,所以|BE|=|AE|,
所以直线AB的倾斜角为![]() ,所以直线AB的斜率为
,所以直线AB的斜率为![]() ,
,
所以直线![]() 的斜率为1,
的斜率为1,
因为点B的坐标为![]() ,所以|BD|=
,所以|BD|=![]() .
.
(2)由题得A(21,0),设直线AB的斜率为![]() ,
,
所以直线AB的方程为![]() ,
,
因为|AC|=|BD|,
所以![]() .
.
由题得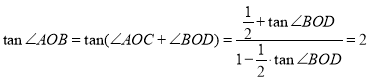 ,
,
所以![]() ,
,
所以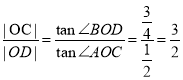 .
.
(3)由题得![]()
![]() ,
,
所以![]() ,
,
所以![]() .
.
因为![]() ,
,
所以![]()
解之得![]() .
.
故![]() 正切值的取值范围为
正切值的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目