题目内容
已知p:|1-
解:由x2-2x+1-m≤0,得1-m≤x≤1+m(m>0),?
所以“![]() q”:A={x∈R|x>1+m或x<1-m,m>0}.?
q”:A={x∈R|x>1+m或x<1-m,m>0}.?
由|1-![]() |≤2,得-2≤x≤10,所以“
|≤2,得-2≤x≤10,所以“![]() p”:B={x∈R|x>10或x<-2}.?
p”:B={x∈R|x>10或x<-2}.?
由![]() p是
p是![]() q的必要而不充分条件知B
q的必要而不充分条件知B![]() A
A![]()
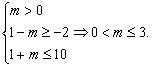
![]() 0<m≤3.?
0<m≤3.?
故m的取值范围为0<m≤3.?
点评:本例“![]() p”是“
p”是“![]() q”的必要不充分条件,即“
q”的必要不充分条件,即“![]() q”
q”![]() “
“![]() p”,但“
p”,但“![]() p”?
p”?![]() “
“![]() q”,可等价转化为“p
q”,可等价转化为“p![]() q”但“q
q”但“q![]() p”,即p是q的充分而非必要条件.实际上,若原命题为“若
p”,即p是q的充分而非必要条件.实际上,若原命题为“若![]() p,则
p,则![]() q”,其逆否命题为“若p则q”.这种思想很重要,要注意灵活应用.本例可用这种等价转化的思想来解答.
q”,其逆否命题为“若p则q”.这种思想很重要,要注意灵活应用.本例可用这种等价转化的思想来解答.

练习册系列答案
相关题目