题目内容
已知函数![]() 的图象在点
的图象在点![]() (e为自然对数的底数)处的切线斜率为3.
(e为自然对数的底数)处的切线斜率为3.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 仅有一个零点,求实数
仅有一个零点,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.

|
|
|
|
| 2 |
|
|
| + | 0 | - | 0 | + |
|
| 增 | 极大值 | 减 | 极小值 | 增 |
………………………………………………………………………………………………6分
由于![]() 时,
时,![]()
![]() ,
,![]()
要使![]() 仅有一个零点,则必须
仅有一个零点,则必须

(3)由![]() 时恒成立
时恒成立
即![]() 恒成立
恒成立
令![]()
![]()
P′![]()
令![]()
当![]() 时,h′
时,h′![]()
∴![]() 上单调递增且函数值由负变正…………………………10分
上单调递增且函数值由负变正…………………………10分
记![]()
则当![]() P′
P′![]() 函数p(x)在(1,x0)上单调递减
函数p(x)在(1,x0)上单调递减
当![]() 时P′
时P′![]() 函数
函数![]() 上单调递增
上单调递增
![]()
又∵![]()
![]()
![]() ……………………………………………………12分
……………………………………………………12分
而![]() 为h(x)的零点,由h(x)在(1,
为h(x)的零点,由h(x)在(1,![]() )的单调递增且由负变正
)的单调递增且由负变正
验证知![]()
![]()
而![]() 上恒成立,知
上恒成立,知
![]() 知
知
∴t最大值为3.……………………………………………………………………………14分

练习册系列答案
相关题目
 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则 .
. 的图象在点
的图象在点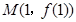 处的切线方程是
处的切线方程是 ,则
,则 ____.
____.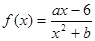 的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0. 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。 的解析式;
的解析式;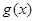 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得 的值域也是
的值域也是 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明); 时,问
时,问 的图象在点
的图象在点 处的切线的方程为
处的切线的方程为 。
。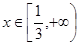 有
有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 在区间
在区间 内有零点,求实数
内有零点,求实数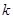 的最大值。
的最大值。