题目内容
20.直线l与椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1$相交于A、B两点,且线段AB的中点为M(1,1),则直线l的方程为x+3y-4=0.分析 通过直线l过点M(1,1)可设其方程为x=m(y-1)+1,并与椭圆方程联立,利用韦达定理及中点坐标公式计算即得结论.
解答 解:依题意,设直线l方程为:x=m(y-1)+1,
联立$\left\{\begin{array}{l}{x=m(y-1)+1}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去x整理得:
(3+m2)y2-2m(m-1)y+m2-2m-8=0,
设A(x1,y1),B(x2,y2),则y1+y2=$\frac{2m(m-1)}{3+{m}^{2}}$,
∵且线段AB的中点为M(1,1),
∴$\frac{2m(m-1)}{3+{m}^{2}}$=2,即m=-3,
∴直线l方程为x=-3(y-1)+1,即x+3y-4=0,
故答案为:x+3y-4=0.
点评 本题考查直线与圆锥曲线的关系,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
10.经过点P(3,-1)且对称轴都在坐标轴上的等轴双曲线的方程是( )
| A. | $\frac{x^2}{10}-\frac{y^2}{10}$=1 | B. | $\frac{y^2}{10}-\frac{x^2}{10}$=1 | C. | $\frac{x^2}{8}-\frac{y^2}{8}$=1 | D. | $\frac{y^2}{8}-\frac{x^2}{8}=1$ |
8.已知f(x)是偶函数,f(-1)=0,f(x)在[0,+∞)上是增函数,则f(x)<0的解集为( )
| A. | (-1,0) | B. | (-1,1) | C. | (0,1) | D. | (-∞,-1) |
12.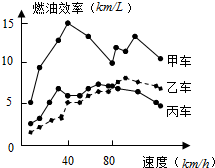 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 无法确定 |
9.设集合A={x丨-2≤x<4},B={x丨x2-ax-4≤0},若B⊆A,则实数a的取值范围为( )
| A. | [-1,2] | B. | [-1,2) | C. | [0,3) | D. | [0,3] |
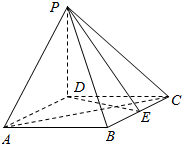 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.