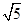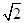题目内容
如图,F1,F2是双曲线C: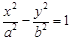 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与 的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3:4 : 5,则双曲线的离心率为
A.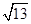 | B.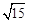 |
| C.2 | D.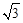 |
A
解析试题分析:∵| AB | : | BF2 | : | AF2 |=3:4 : 5,不妨令|AB|=3,| BF2 | =4,|AF2|=5,
∵|AB|2+ | BF2 | 2=|AF2|2,∴∠ABF2=90°,又由双曲线的定义得:|BF1|-|BF2|=2a,|AF2|-|AF1|=2a,
∴|AF1|+3-4=5-|AF1|,∴|AF1|=3.∴|BF1|-|BF2|=3+3-4=2a,∴a=1.
在Rt△BF1F2中,|F1F2|2=|BF1|2+|BF2|2=62+42=52,又|F1F2|2=4c2,∴4c2=52,∴c=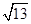 .
.
∴双曲线的离心率e=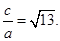
考点:本小题主要考查双曲线的几何性质.
点评:本题考查转化思想与运算能力,其中求得a与c的值是关键,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
动点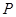 到两定点
到两定点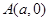 ,
,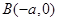 连线的斜率的乘积为
连线的斜率的乘积为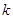 (
(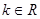 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
过点 且与抛物线
且与抛物线 只有一个公共点的直线有( ).
只有一个公共点的直线有( ).
A. 条 条 | B. 条 条 | C.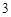 条 条 | D. 条 条 |
知圆柱的底面半径为2,高为3,用一个平面去截,若所截得的截面为椭圆,则椭圆的离心率的取值范围为( )
A. | B.(0, | C. | D.(0,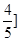 |
抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当 为等边三角形时,其面积为
为等边三角形时,其面积为
A. | B.4 | C.6 | D.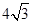 |
若双曲线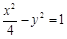 的渐近线与圆
的渐近线与圆 (
(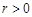 )相切,则
)相切,则
| A.5 | B.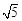 | C.2 | D. |
若双曲线 的离心率是2,则实数k的值是 ( )
的离心率是2,则实数k的值是 ( )
| A.—3 | B.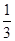 | C.3 | D.—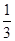 |
 ,则双曲线的的离心率为( )
,则双曲线的的离心率为( )

 (
(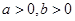 )的右焦点
)的右焦点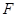 作圆
作圆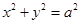 的切线
的切线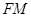 ,交
,交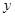 轴于点
轴于点 ,切圆于点
,切圆于点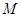 ,若
,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )