题目内容
已知P(x,y)为函数y=lnx图象上一点,O为坐标原点,记直线OP的斜率f(x).
(Ⅰ)求f(x)的最大值;
(Ⅱ)令g(x)=x2-ax•f(x),试讨论函数g(x)在区间(1,ea)上零点的个数(e为自然对数的底数,e=2.71828…).
(Ⅰ)求f(x)的最大值;
(Ⅱ)令g(x)=x2-ax•f(x),试讨论函数g(x)在区间(1,ea)上零点的个数(e为自然对数的底数,e=2.71828…).
分析:(Ⅰ)由题意知f(x)=
,利用导数法判断函数的单调性后,可得f(x)在(0,e)上递增;f(x)在(e,+∞)上递减;故f(x)的最大值为f(e)
(II)由区间的定义可得a>0,且ea-a>0,求出函数g(x)的函数解析式,利用导数法分析其单调性后,分①当
(1-ln
)>0,即0<a<2e时,
②当
(1-ln
)=0,即a=2e时,③当
(1-ln
)<0,即a>2e时,三种情况讨论函数g(x)在区间(1,ea)上零点的个数,最后综合讨论结果,可得答案.
| lnx |
| x |
(II)由区间的定义可得a>0,且ea-a>0,求出函数g(x)的函数解析式,利用导数法分析其单调性后,分①当
| a |
| 2 |
| a |
| 2 |
②当
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:解:(Ⅰ)由题意知f(x)=
,
∴f′(x)=
当x∈(0,e)时,f′(x)>0,f(x)在(0,e)上递增;
当x∈(e,+∞)时,f′(x)<0,f(x)在(e,+∞)上递减;
所以,f(x)的最大值为f(e)=
.…(4分)
(Ⅱ)∵ea>1
∴a>0,且ea-a>0
因为g(x)=x2-ax•f(x)=g(x)=x2-alnx,
所以g′(x)=2x-
=
=
.
当x∈(0,
)时,g′(x)<0,当x∈(
,+∞)时,g′(x)>0,
所以g(x)在(0,
)上是减函数,在(
,+∞)上是增函数.
所以,当x=
时,g(x)取最小值g(
)=
(1-ln
) …(7分)
下面讨论函数g(x)的零点情况.
①当
(1-ln
)>0,即0<a<2e时,
函数g(x)在(1,ea)上无零点;
②当
(1-ln
)=0,即a=2e时,
=
,
又
<a<ea<e2a
∴
<ea,则1<
<ea,
而g(1)=1>0,g(
)=0,g(ea)>0
∴g(x)在(1,ea)上有一个零点;
③当
(1-ln
)<0,即a>2e时,ea>
>
>1,
由于g(1)=1>0,g(
)=
(1-ln
)<0,
g(ea)>e2a-alnea=e2a-a2=(ea-a)(ea+a)>0,
所以,函数g(x)在(1,ea)上有两个零点.
综上所述,g(x)在(1,ea)上,有结论:
当0<a<2e时,函数g(x)无零点;
当a=2e 时,函数g(x)有一个零点;
当a>2e时,函数g(x)有两个零点.…(10分)
| lnx |
| x |
∴f′(x)=
| 1-lnx |
| x2 |
当x∈(0,e)时,f′(x)>0,f(x)在(0,e)上递增;
当x∈(e,+∞)时,f′(x)<0,f(x)在(e,+∞)上递减;
所以,f(x)的最大值为f(e)=
| 1 |
| e |
(Ⅱ)∵ea>1
∴a>0,且ea-a>0
因为g(x)=x2-ax•f(x)=g(x)=x2-alnx,
所以g′(x)=2x-
| a |
| x |
| 2x2-a |
| x |
2(x-
| ||||||||
| x |
当x∈(0,
| ||
| x |
| ||
| x |
所以g(x)在(0,
| ||
| x |
| ||
| x |
所以,当x=
| ||
| x |
| ||
| x |
| a |
| 2 |
| a |
| 2 |
下面讨论函数g(x)的零点情况.
①当
| a |
| 2 |
| a |
| 2 |
函数g(x)在(1,ea)上无零点;
②当
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| e |
又
| a |
| 2 |
∴
| ||
| 2 |
| ||
| 2 |
而g(1)=1>0,g(
| ||
| 2 |
∴g(x)在(1,ea)上有一个零点;
③当
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| e |
由于g(1)=1>0,g(
| ||
| x |
| a |
| 2 |
| a |
| 2 |
g(ea)>e2a-alnea=e2a-a2=(ea-a)(ea+a)>0,
所以,函数g(x)在(1,ea)上有两个零点.
综上所述,g(x)在(1,ea)上,有结论:
当0<a<2e时,函数g(x)无零点;
当a=2e 时,函数g(x)有一个零点;
当a>2e时,函数g(x)有两个零点.…(10分)
点评:本题考查的知识点是利用导数求闭区间上的最值,利用导数研究函数的极值,是导数问题比较综合的应用,难度较大,特别是第(II)问中分类标准的确定,一定要引起足够的重视.

练习册系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )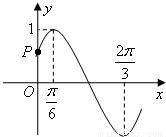



 -2lnx、
-2lnx、