题目内容
 某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合.
某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合.
(1)将A,B两点间的直线距离d(cm)表示成时间t(s)的函数,其中t∈[0,60];
(2)若h(t)= ,其中t∈[0,30],求出函数h(t)的所有最高点坐标.
,其中t∈[0,30],求出函数h(t)的所有最高点坐标.
解:(1)∵∠AOB= ×2π=
×2π=
∴由余弦定理可得|AB|= =10cos
=10cos ,t∈[0,60];
,t∈[0,60];
(2)h(t)= =
= =
= ,其中t∈[0,30],
,其中t∈[0,30],
∴cos =1时,,h(t)取得最大值为
=1时,,h(t)取得最大值为
此时, (k∈Z),∴t=6kπ
(k∈Z),∴t=6kπ
∵t∈[0,30],∴t=0或6π
即函数h(t)的所有最高点坐标为(0, )或(6π,
)或(6π, ).
).
分析:(1)确定∠AOB,利用余弦定理,可求A,B两点间的直线距离d(cm)表示成时间t(s)的函数;
(2)利用余弦函数的最值,可得结论.
点评:本题考查余弦定理的运用,考查三角函数的化简,考查学生的计算能力,属于中档题.
 ×2π=
×2π=
∴由余弦定理可得|AB|=
 =10cos
=10cos ,t∈[0,60];
,t∈[0,60];(2)h(t)=
 =
= =
= ,其中t∈[0,30],
,其中t∈[0,30],∴cos
 =1时,,h(t)取得最大值为
=1时,,h(t)取得最大值为
此时,
 (k∈Z),∴t=6kπ
(k∈Z),∴t=6kπ∵t∈[0,30],∴t=0或6π
即函数h(t)的所有最高点坐标为(0,
 )或(6π,
)或(6π, ).
).分析:(1)确定∠AOB,利用余弦定理,可求A,B两点间的直线距离d(cm)表示成时间t(s)的函数;
(2)利用余弦函数的最值,可得结论.
点评:本题考查余弦定理的运用,考查三角函数的化简,考查学生的计算能力,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
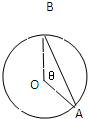 某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合.
某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合.