题目内容
函数f(x)=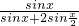 是以 ________为最小正周期的 ________(选填“奇”或“偶”)函数.
是以 ________为最小正周期的 ________(选填“奇”或“偶”)函数.
4π 偶函数
分析:先利用二倍角公式对函数解析式进行化简整理,进而利用余弦函数的性质求得函数的最小正周期和奇偶性.
解答:f(x)=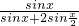 =
= =
= =1-
=1-
∴y=cos 的最小正周期T=
的最小正周期T=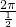 =4π,为偶函数
=4π,为偶函数
∴函数f(x)的最小正周期为4π,偶函数
故答案为:4π,偶函数
点评:本题主要考查了三角函数的周期性及其求法,余弦函数的基本性质.考查了学生对三角函数基础知识的整体把握.
分析:先利用二倍角公式对函数解析式进行化简整理,进而利用余弦函数的性质求得函数的最小正周期和奇偶性.
解答:f(x)=
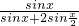 =
= =
= =1-
=1-
∴y=cos
 的最小正周期T=
的最小正周期T=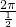 =4π,为偶函数
=4π,为偶函数∴函数f(x)的最小正周期为4π,偶函数
故答案为:4π,偶函数
点评:本题主要考查了三角函数的周期性及其求法,余弦函数的基本性质.考查了学生对三角函数基础知识的整体把握.

练习册系列答案
相关题目
定义在R上的函数f(x)满足:f(x+2)+f(x)=0,且函数f(x+1)为奇函数,对于下列命题:
①函数f(x)是以T=2为周期的函数;
②函数f(x)的图象关于点(1,0)对称;
③函数f(x)的图象关于直线x=2对称;
④函数f(x)的最大值为f(2);
⑤f(2011)=0.
其中正确结论的序号为( )
①函数f(x)是以T=2为周期的函数;
②函数f(x)的图象关于点(1,0)对称;
③函数f(x)的图象关于直线x=2对称;
④函数f(x)的最大值为f(2);
⑤f(2011)=0.
其中正确结论的序号为( )
| A、①③⑤ | B、②③⑤ | C、②③④ | D、①④⑤ |
已知函数y=f(x)?sinx是以π为周期的奇函数,则f(x)可以是( )
| A、sin2x | B、cos2x | C、sinx | D、cosx |