题目内容
若二阶矩阵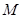 满足:
满足: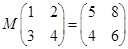 .
.
(1)求二阶矩阵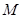 ;
;
(2)若曲线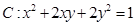 在矩阵
在矩阵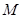 所对应的变换作用下得到曲线
所对应的变换作用下得到曲线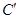 ,求曲线
,求曲线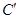 的方程.
的方程.
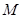 满足:
满足: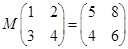 .
.(1)求二阶矩阵
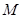 ;
;(2)若曲线
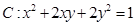 在矩阵
在矩阵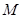 所对应的变换作用下得到曲线
所对应的变换作用下得到曲线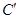 ,求曲线
,求曲线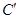 的方程.
的方程.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)由二阶矩阵
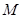 满足:
满足: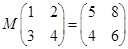 ,假设
,假设 ,求出相应的矩阵A对应的行列式,即可求出矩阵A的逆矩阵,所以矩阵M等于矩阵
,求出相应的矩阵A对应的行列式,即可求出矩阵A的逆矩阵,所以矩阵M等于矩阵 与矩阵A的逆矩阵
与矩阵A的逆矩阵 相乘,可得
相乘,可得 .
.(2)假设曲线曲线
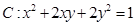 上任一点,求出该点在矩阵的作用下的对应的点,根据坐标关系求出对应点的方程.
上任一点,求出该点在矩阵的作用下的对应的点,根据坐标关系求出对应点的方程.(1)设
 ,则
,则 ,
, , 2分
, 2分 . 3分
. 3分(2)
 ,
,即
 4分
4分代入
 可得
可得 ,即
,即 ,
,故曲线
 的方程为
的方程为 . 7分
. 7分
练习册系列答案
相关题目
 的逆矩阵
的逆矩阵 .
. 的特征值以及属于每个特征值的一个特征向量.
的特征值以及属于每个特征值的一个特征向量. (
( ,
, 为实数).若矩阵
为实数).若矩阵 属于特征值2,3的一个特征向量分别为
属于特征值2,3的一个特征向量分别为 ,
, ,求矩阵
,求矩阵 的逆矩阵
的逆矩阵 .
.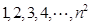 (
(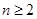 )任意排成
)任意排成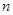 行
行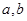 (
(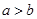 )的比值
)的比值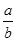 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若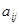 表示某个
表示某个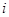 行第
行第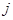 列的数(
列的数(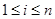 ,
,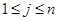 ),且满足
),且满足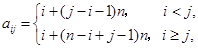 ,当
,当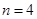 时数表的“特征值”为_________
时数表的“特征值”为_________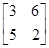 的特征值及相应的特征向量.
的特征值及相应的特征向量.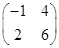 的特征值和特征向量.
的特征值和特征向量. (a,b,c,d∈{-1,1,2})的所有可能值中,最大的是 .
(a,b,c,d∈{-1,1,2})的所有可能值中,最大的是 .