题目内容
已知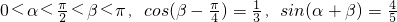 ,则
,则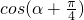 =________.
=________.

分析:利用α+
 =(α+β)-(β-
=(α+β)-(β- ),从而由两角差的余弦即可求得答案.
),从而由两角差的余弦即可求得答案.解答:∵0<α<
 <β,
<β,∴
 <β-
<β- <
< ,
,又cos(β-
 )=
)= ,
,∴sin(β-
 )=
)= ;
;同理可得
 <α+β<
<α+β< ,又sin(α+β)=
,又sin(α+β)= ,
,∴cos(α+β)=-
 ;
;∴cos(α+
 )=cos[(α+β)-(β-
)=cos[(α+β)-(β- )]
)]=cos(α+β)•cos(β-
 )+sin(α+β)•sin(β-
)+sin(α+β)•sin(β- )
)=-
 ×
× +
+ ×
×
=
 .
.故答案为:
 .
.点评:本题考查三角函数的恒等变换及化简求值,考查两角差的余弦,突出考查观察与运算能力,属于中档题.

练习册系列答案
相关题目
 ,则f(1)= .
,则f(1)= . ,则f(2)+f(-2)的值为( )
,则f(2)+f(-2)的值为( ) ,则
,则 的值为 .
的值为 . ,
, ,
, 为三个向量,则•
为三个向量,则• =
= •”;
•”; ;
; ,则a1+a2+…a8=256
,则a1+a2+…a8=256 ,则
,则 。
。