题目内容
已知椭圆 的右焦点F(1,0),离心率为
的右焦点F(1,0),离心率为 .过点F的直线l交椭圆C于A,B两点,且
.过点F的直线l交椭圆C于A,B两点,且 .
.(1)求椭圆C的方程;
(2)求直线l的斜率的取值范围.
【答案】分析:(1)利用椭圆的离心率公式、关系式a2=b2+c2即可得出a、b,进而得到椭圆的标准方程;
(2)把直线的方程与椭圆的方程联立,利用根与系数的关系及已知条件即可得出斜率的取值范围.
解答:解:(1)由已知得: ,
,
∴a=2,b2=a2-c2=3,
∴椭圆C的方程为
(2)设直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2).
由 ,
,
得(3+4k2)x2-8k2x+4k2-12=0,
∵直线l过焦点F,∴△>0,
且 ,
,
∴ ,
,
同理 ,
,
故|FA|•|FB|=(1+k2)|(x1-1)(x2-1)|= .
.
由 ,∴
,∴ ,解得0≤k2≤2.
,解得0≤k2≤2.
所以直线l的斜率k的取值范围是 .
.
点评:熟练掌握椭圆的定义及性质、直线与椭圆的相交问题的解题方法、根与系数的关系、不等式的解法是解题的关键.
(2)把直线的方程与椭圆的方程联立,利用根与系数的关系及已知条件即可得出斜率的取值范围.
解答:解:(1)由已知得:
 ,
,∴a=2,b2=a2-c2=3,
∴椭圆C的方程为

(2)设直线l的方程为y=k(x-1),A(x1,y1),B(x2,y2).
由
 ,
,得(3+4k2)x2-8k2x+4k2-12=0,
∵直线l过焦点F,∴△>0,
且
 ,
,∴
 ,
,同理
 ,
,故|FA|•|FB|=(1+k2)|(x1-1)(x2-1)|=
 .
.由
 ,∴
,∴ ,解得0≤k2≤2.
,解得0≤k2≤2.所以直线l的斜率k的取值范围是
 .
.点评:熟练掌握椭圆的定义及性质、直线与椭圆的相交问题的解题方法、根与系数的关系、不等式的解法是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
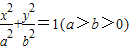 的右焦点F(1,0),离心率为e.
的右焦点F(1,0),离心率为e.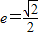 ,求椭圆方程;
,求椭圆方程;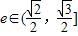 时,求k的取值范围.
时,求k的取值范围.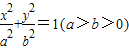 的右焦点F(1,0),离心率为e.
的右焦点F(1,0),离心率为e.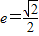 ,求椭圆方程;
,求椭圆方程;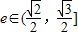 时,求k的取值范围.
时,求k的取值范围.