题目内容
在△ABC中,若
=
=
,则△ABC的形状是( )
| a | ||
sin
|
| b | ||
sin
|
| c | ||
sin
|
| A、等边三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、直角三角形 |
分析:根据正弦定理,将条件进行化简,
解答:解:根据正弦定理可知
=
=
,
等价为
=
=
,
即
=
=
,
∴cos?
=cos?
=cos?
,
在三角形ABC中,可知
=
=
,
∴A=B=C.
故三角形ABC是等边三角形.
故选:A.
| a | ||
sin
|
| b | ||
sin
|
| c | ||
sin
|
等价为
| sin?A | ||
sin?
|
| sin?B | ||
sin?
|
| sin?C | ||
sin?
|
即
2sin?
| ||||
sin?
|
2sin?
| ||||
sin?
|
2sin?
| ||||
sin?
|
∴cos?
| A |
| 2 |
| B |
| 2 |
| C |
| 2 |
在三角形ABC中,可知
| A |
| 2 |
| B |
| 2 |
| C |
| 2 |
∴A=B=C.
故三角形ABC是等边三角形.
故选:A.
点评:本题主要考查三角形的形状的判断,利用正弦定理和三角函数的倍角公式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC、AC的中点,SA=SC= ,BC=
,BC= AC,∠ASC=∠ACB=90°.
AC,∠ASC=∠ACB=90°.
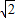 ,BC=
,BC= AC,∠ASC=∠ACB=90°.
AC,∠ASC=∠ACB=90°.