Question

定义区间（m，n），[m，n]，[m，n），（m，n]的长度均为n-m，其中n＞m，已知关于x的不等式组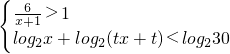的解集构成的各区间的长度和为5，则实数t的取值范围是

1. A.
   （0，1]
2. B.
   [1，+∞）
3. C.
   （0，5]
4. D.
   [5，+∞）

Answer 1

A
分析：先解关于x的不等式组，解出两个不等式的解集，求两个不等式的解集的交集，A∩B⊆（0，5），不等式组的解集的各区间长度和为5，写出不等式组进行讨论，得到结果．
解答：先解不等式，整理得，即（x+1）•（x-5）＜0，
所以不等式 的解集A=（-1，5）
设不等式log₂x+log₂（tx+t）＜log₂30 的解集为B，则不等式组的解集为A∩B．
不等式log₂x+log₂（tx+t）＜log₂30 等价于 ．
又A∩B⊆（0，5），不等式组的解集的各区间长度和为6，所以不等式组 ，当x∈（0，5）时，恒成立．
当x∈（0，5）时，不等式tx+t＞0恒成立，得t＞0．①（13分）
当x∈（0，5）时，不等式tx²+tx-30＜0恒成立，即 恒成立．
而当x∈（0，5）时，的取值范围为 （1，+∞），所以实数 t≤1，②
综合①②可得，t的取值范围为 （0，1]，
故选A．
点评：本题考查一个新定义问题，即区间的长度，本题解题的关键是对于条件中所给的三种不同的题目进行整理变化，注意恒成立问题，这是高考题目中必出的．