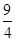题目内容
(本小题满分13分)设数列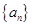 的前项和为
的前项和为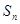 ,且
,且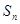
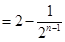 ,
,
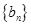 为等差数列,且
为等差数列,且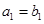 ,
,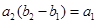 .
.
(Ⅰ)求数列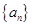 和
和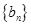 通项公式;
通项公式;
(Ⅱ)设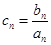 ,求数列
,求数列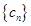 的前
的前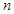 项和
项和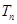 .
.
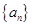 的前项和为
的前项和为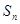 ,且
,且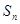
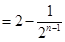 ,
,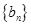 为等差数列,且
为等差数列,且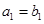 ,
,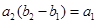 .
.(Ⅰ)求数列
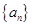 和
和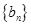 通项公式;
通项公式;(Ⅱ)设
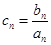 ,求数列
,求数列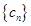 的前
的前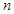 项和
项和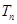 .
.(1)当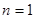 时,
时,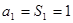 .…………1分
.…………1分
当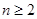 时,
时,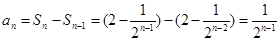 ,…………3分
,…………3分
此式对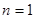 也成立.
也成立. 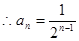
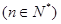 .………………………4分 ,
.………………………4分 ,
从而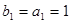 ,
,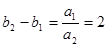 .又因为
.又因为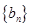 为等差数列,
为等差数列,
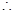 公差
公差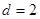 ,……………………………………………………………… 5分
,……………………………………………………………… 5分
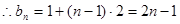 .………………………………………………6分
.………………………………………………6分
(2)由(1)可知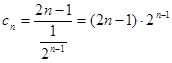 ,…………………………7分
,…………………………7分
所以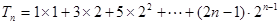 .①
.①
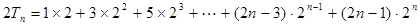 .②……9分
.②……9分
①-②得:
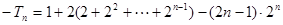
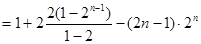
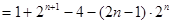
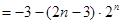 .………………………………………………12分
.………………………………………………12分
 .…………………………………………………13分
.…………………………………………………13分
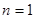 时,
时,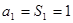 .…………1分
.…………1分当
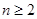 时,
时,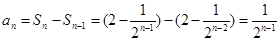 ,…………3分
,…………3分此式对
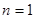 也成立.
也成立. 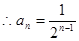
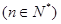 .………………………4分 ,
.………………………4分 ,从而
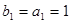 ,
,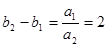 .又因为
.又因为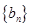 为等差数列,
为等差数列,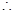 公差
公差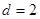 ,……………………………………………………………… 5分
,……………………………………………………………… 5分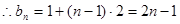 .………………………………………………6分
.………………………………………………6分(2)由(1)可知
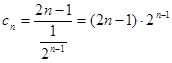 ,…………………………7分
,…………………………7分所以
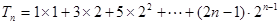 .①
.①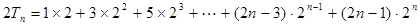 .②……9分
.②……9分①-②得:
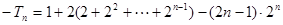
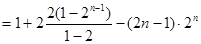
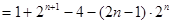
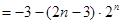 .………………………………………………12分
.………………………………………………12分 .…………………………………………………13分
.…………………………………………………13分试题分析:(Ⅰ)由an=
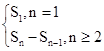 可求数列{an}的通项公式,进而可求数列{bn}通项公式;
可求数列{an}的通项公式,进而可求数列{bn}通项公式;(Ⅱ)由(Ⅰ)可知cn=(2n-1)•2n-1,故可用错位相减法来求数列的前n项和.
点评:解决该试题的易错点是错位相减法的准确求解,尤其是项数的确定问题。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
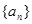 中,
中,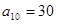 ,
,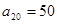 .
.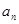 ;
;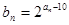 ,证明:数列
,证明:数列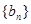 为等比数列;
为等比数列;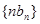 的前
的前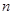 项和
项和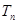 .
.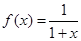 ,各项均为正数的数列
,各项均为正数的数列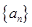 满足
满足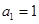 ,
,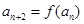 ,若
,若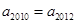 ,则
,则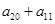 的值是 .
的值是 .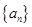 满足:
满足: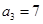 ,
,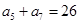 ,
,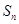 .
.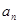 及;
及;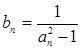 (n
(n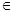 N*),求数列
N*),求数列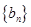 的前n项和
的前n项和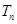 .
.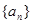 是非零等差数列,又
是非零等差数列,又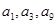 组成一个等比数列的前三项,则
组成一个等比数列的前三项,则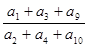 的值是 .
的值是 .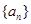 中,
中,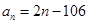 ,则使前n项和
,则使前n项和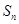 取得最小值的n的值为
取得最小值的n的值为 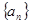 满足:
满足: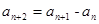 (
(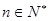 ),且
),且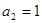 ,若数列的前2011项之
,若数列的前2011项之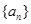 为等差数列,
为等差数列,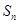 为其前
为其前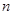 项和,若
项和,若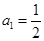 ,
,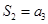 ,则
,则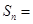 ___________.
___________.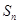 为等差数列
为等差数列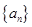 的前
的前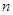 项和,若
项和,若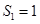 ,
,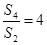 ,则
,则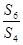 的值为( )
的值为( )