题目内容
在平面直角坐标系xOy中,已知圆心在第二象限,半径为2 的圆C与直线y=x相切于坐标原点O.
的圆C与直线y=x相切于坐标原点O.
(1)求圆C的方程;
(2)试探求C上是否存在异于原点的点Q,使Q到定点F(4,0)的距离等于线段OF的长.若存在,请求出点Q的坐标;若不存在,请说明理由.
解:(1)设圆C的圆心为C(a,b),则圆C的方程为(x-a)2+(y-b)2=8,
∵直线y=x与圆C相切于坐标原点O.
∴O点在圆C上,
且OC垂直于直线y=x,
于是有
由于点C(a,b)在第二象限,故a<0,b>0.
∴a=-2,b=2.
∴圆C的方 程为(x+2)2+(y-2)2=8.
程为(x+2)2+(y-2)2=8.
(2)假设存在点Q符合要求,设Q(x,y),
则有
解之得x= 或x=0(舍去).
或x=0(舍去).
∴y= .
.
所以存在点Q ,使Q到定点F(4,0)的距离等于线段OF的长.
,使Q到定点F(4,0)的距离等于线段OF的长.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 +1=0的距离是( )
+1=0的距离是( ) B.
B.
 D.
D.
 .
. ,则两圆心的距离|C1C2|=( )
,则两圆心的距离|C1C2|=( )
 |
| MN|≥2
MN|≥2 ,则k的取值范围是( )
,则k的取值范围是( )
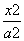 -
-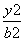 =1(a,b>0)的两
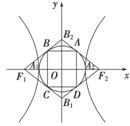
=1(a,b>0)的两 顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D.则
顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D.则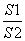 =________.
=________.
 的线段AB的两个端点A、B分别在x轴、y轴上滑动,P是AB上一点,且
的线段AB的两个端点A、B分别在x轴、y轴上滑动,P是AB上一点,且 =
=
 ,求点P的轨迹C的方程.
,求点P的轨迹C的方程.