题目内容
已知四边形ABCD内接于圆,AC与BD相交于点M,∠ADB=60°,∠CBD=15°,BC=
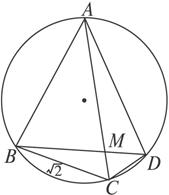
解:如图,在△AMD中,依正弦定理,得![]()
∵∠CAD=∠CBD=15°,∠ADB=60°,
∴∠AMD=180°-75°=105°.
∴DM=![]() =(1+
=(1+![]() )(2-
)(2-![]() )=
)=![]() -1.
-1.
在△BCM中,BM=![]() =3-
=3-![]() .
.
在△ABD中,BD=BM+MD=3-![]() +
+![]() -1=2.
-1=2.
依据余弦定理,得AB2=AD2+BD2-?2AD·BD·cos∠ADB=4+2![]() +4-2(1+
+4-2(1+![]() )=6.
)=6.
∴AB=![]() .
.
温馨提示
对几何问题的解决,将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理,余弦定理等有关知识正确求解,演算过程要算法简练,计算准确,最后作答.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (2013•牡丹江一模)选修4-1:几何证明选讲
(2013•牡丹江一模)选修4-1:几何证明选讲 (几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切
(几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切 (2012•南京一模)选修4-1:几何证明选讲
(2012•南京一模)选修4-1:几何证明选讲 (2013•辽宁一模)如图已知四边形ABCD内接于⊙O,DA与CB的延长线交于点E,且EF∥CD,AB的延长线与EF相交于点F,FG切⊙O于点G.
(2013•辽宁一模)如图已知四边形ABCD内接于⊙O,DA与CB的延长线交于点E,且EF∥CD,AB的延长线与EF相交于点F,FG切⊙O于点G.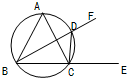 如图,已知四边形ABCD内接于圆,延长AD,BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF,若AC=3cm,AD=2cm,则DE长为
如图,已知四边形ABCD内接于圆,延长AD,BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF,若AC=3cm,AD=2cm,则DE长为