题目内容
已知一个动圆与圆C:(x+4)2+y2=100相内切,且过点A(4,0),求这个动圆圆心的轨迹方程.分析:利用两个圆相内切的充要条件得到动点的几何关系,利用椭圆的定义判断出其轨迹为椭圆,据椭圆的标准方程求出这个动圆圆心的轨迹方程.
解答:解:设动圆圆为M(x,y),半径为r
那么
∴|MC|+|MA|=10>|AC|=8
因此点M的轨迹是以A、C为焦点,长轴长为10的椭圆.
其中a=5,c=4,b=3
其方程是:
+
=1.
那么
|
∴|MC|+|MA|=10>|AC|=8
因此点M的轨迹是以A、C为焦点,长轴长为10的椭圆.
其中a=5,c=4,b=3
其方程是:
| x2 |
| 25 |
| y2 |
| 9 |
点评:求动点的轨迹方程问题,应该首先根据动点满足的几何条件判断是否是一些特殊的曲线,若是,直接据定义求出轨迹方程即可.

练习册系列答案
相关题目
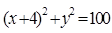 相内切,且过点A(4,0),则这个动圆圆心的轨迹方程是_______________.
相内切,且过点A(4,0),则这个动圆圆心的轨迹方程是_______________.