题目内容
已知向量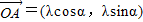 (λ≠0),
(λ≠0),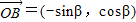 ,其中O为坐标原点.
,其中O为坐标原点.(Ⅰ)若α-β=
 且λ=1,求向量
且λ=1,求向量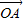 与
与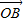 的夹角;
的夹角;(Ⅱ)若不等式|
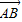 |≥2|
|≥2|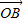 |对任意实数α,β都成立,求实数λ的取值范围.
|对任意实数α,β都成立,求实数λ的取值范围.
【答案】分析:(Ⅰ)λ=1时,利用向量模的坐标公式求出向量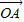 、
、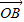 的长度,从而得到
的长度,从而得到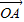 •
•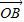 =cosθ,然后利用向量数理积的坐标公式,得到
=cosθ,然后利用向量数理积的坐标公式,得到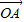 •
•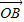 =sin(β-α)=
=sin(β-α)= ,最后解关于夹角θ的方程,可得向量
,最后解关于夹角θ的方程,可得向量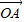 与
与 的夹角;
的夹角;
(Ⅱ)代入(1)的运算结果,将不等式|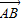 |≥2|
|≥2|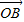 |整理为:λ2-2λsin(β-α)+1≥4对任意实数α、β都成立,再结合正弦函数的有界性,建立关于λ的不等式组,解之可得满足条件的实数λ的取值范围.
|整理为:λ2-2λsin(β-α)+1≥4对任意实数α、β都成立,再结合正弦函数的有界性,建立关于λ的不等式组,解之可得满足条件的实数λ的取值范围.
解答:解:(Ⅰ)当λ=1时,
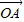 =(cosα,sinα),
=(cosα,sinα),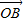 =(-sinβ,cosβ)
=(-sinβ,cosβ)
∴|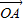 |=1,|
|=1,|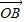 |=1
|=1
设向量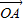 与
与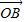 的夹角为θ,得
的夹角为θ,得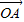 •
•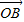 =|
=|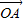 ||
||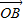 |cosθ=cosθ
|cosθ=cosθ
又∵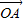 •
• =cosα(-sinβ)+(sinα)cosβ=sin(α-β)=sin
=cosα(-sinβ)+(sinα)cosβ=sin(α-β)=sin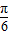 =
=
∴cosθ=
∵θ∈[0,π]
∴θ=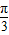
(Ⅱ)|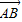 |2=|
|2=| -
-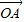 |2=|
|2=|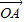 |2-2
|2-2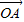 •
•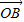 +|
+|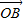 |2=λ2-2λsin(α-β)+1
|2=λ2-2λsin(α-β)+1
不等式|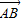 |≥2|
|≥2|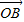 |可化为:λ2-2λsin(α-β)+1≥4,
|可化为:λ2-2λsin(α-β)+1≥4,
即λ2-2λsin(α-β)-3≥0对任意实数α、β都成立
∵-1≤sin(α-β)≤1
∴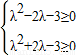
解得:λ≤-3或λ≥3
∴实数λ的取值范围是(-∞,-3]∪[3,+∞)
点评:本题综合了平面向量的数量积、和与差的三角函数以及不等式恒成立等知识点,属于难题.解题时应该注意等价转化和函数方程思想的运用.
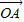 、
、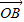 的长度,从而得到
的长度,从而得到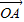 •
•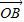 =cosθ,然后利用向量数理积的坐标公式,得到
=cosθ,然后利用向量数理积的坐标公式,得到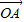 •
•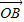 =sin(β-α)=
=sin(β-α)= ,最后解关于夹角θ的方程,可得向量
,最后解关于夹角θ的方程,可得向量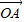 与
与 的夹角;
的夹角;(Ⅱ)代入(1)的运算结果,将不等式|
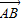 |≥2|
|≥2|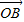 |整理为:λ2-2λsin(β-α)+1≥4对任意实数α、β都成立,再结合正弦函数的有界性,建立关于λ的不等式组,解之可得满足条件的实数λ的取值范围.
|整理为:λ2-2λsin(β-α)+1≥4对任意实数α、β都成立,再结合正弦函数的有界性,建立关于λ的不等式组,解之可得满足条件的实数λ的取值范围.解答:解:(Ⅰ)当λ=1时,
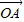 =(cosα,sinα),
=(cosα,sinα),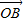 =(-sinβ,cosβ)
=(-sinβ,cosβ)∴|
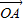 |=1,|
|=1,|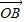 |=1
|=1设向量
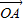 与
与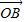 的夹角为θ,得
的夹角为θ,得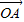 •
•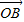 =|
=|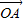 ||
||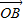 |cosθ=cosθ
|cosθ=cosθ又∵
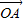 •
• =cosα(-sinβ)+(sinα)cosβ=sin(α-β)=sin
=cosα(-sinβ)+(sinα)cosβ=sin(α-β)=sin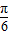 =
=
∴cosθ=

∵θ∈[0,π]
∴θ=
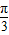
(Ⅱ)|
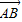 |2=|
|2=| -
-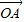 |2=|
|2=|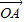 |2-2
|2-2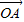 •
•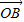 +|
+|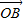 |2=λ2-2λsin(α-β)+1
|2=λ2-2λsin(α-β)+1不等式|
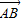 |≥2|
|≥2|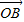 |可化为:λ2-2λsin(α-β)+1≥4,
|可化为:λ2-2λsin(α-β)+1≥4,即λ2-2λsin(α-β)-3≥0对任意实数α、β都成立
∵-1≤sin(α-β)≤1
∴
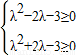
解得:λ≤-3或λ≥3
∴实数λ的取值范围是(-∞,-3]∪[3,+∞)
点评:本题综合了平面向量的数量积、和与差的三角函数以及不等式恒成立等知识点,属于难题.解题时应该注意等价转化和函数方程思想的运用.

练习册系列答案
相关题目
已知向量
=(0,2,1),
=(-1,1,-2),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、0° | B、45° |
| C、90° | D、180° |