题目内容
 已知F为抛物线C1:x2=2py(p>0)的焦点,若过焦点F的直线l交C1于A,B两点,使抛物线C1在点A,B处的两条切线的交点M恰好在圆C2:x2+y2=8上.
已知F为抛物线C1:x2=2py(p>0)的焦点,若过焦点F的直线l交C1于A,B两点,使抛物线C1在点A,B处的两条切线的交点M恰好在圆C2:x2+y2=8上.(I)当p=2时,求点M的坐标;
(II)求△MAB面积的最小值及取得最小值时的抛物线C1的方程.
分析:(Ⅰ)通过求导即可得到切线的斜率,联立切线的方程即可求得交点M的坐标,联立直线l的方程与抛物线的方程,利用根与系数的关系进一步化简得到点M的坐标,再代入圆的方程即可得出;
(Ⅱ)相交、相切的解法同上,再利用弦长公式、点到直线的距离公式即可得到三角形的面积表达式,利用导数即可求出其最小值.
(Ⅱ)相交、相切的解法同上,再利用弦长公式、点到直线的距离公式即可得到三角形的面积表达式,利用导数即可求出其最小值.
解答:解:(Ⅰ)∵p=2,∴抛物线C1的方程为x2=4y,∴焦点F(0,1).
设直线l的方程为y=kx+1,点A(x1,y1),B(x2,y2).
对x2=4y求导得y′=
,∴切线MA,MB的方程分别为y=
x-
,y=
x-
.
联立
,解得
,即点M(
,
).
联立
,消去y得到x2-4kx-4=0,显然△>0.
∴x1+x2=4k,x1x2=-4,∴点M(2k,-1).
把点M的坐标代入圆C2的方程得4k2+1=8,解得k=±
,
∴点M(±
,-1).
(Ⅱ)是直线l的方程为y=kx+
,点A(x1,y1),B(x2,y2).
对x2=2py求导得y′=
,
∴切线MA,MB的方程分别为y=
x-
,y=
x-
,联立解得交点M(
,
)..
由
得x2-2pkx-p2=0,得到x1+x2=2pk,x1x2=-p2.
∴点M(pk,-
),代入圆C2的方程得p2k2+
=8,(*)
又弦长|AB|=
=
=2p(1+k2).
点M到直线l的距离d=
=p
.
∴S△MAB=
×2p(1+k2)×p
=p2(1+k2)
.
由(*)得p2=
,代入上式整理得S△MAB=
.
令1+k2=t≥1,则S△MAB=
,则S′(t)=
,
∵在区间[1,
)上,S′(t)<0,∴S(t)单调递减;
∵在区间(
,+∞)上,S′(t)>0,∴S(t)单调递增.
∴当t=
,即k2=
,p2=
时,(S△MAB)min=18.
此时抛物线的方程为x2=
y.
设直线l的方程为y=kx+1,点A(x1,y1),B(x2,y2).
对x2=4y求导得y′=
| x |
| 2 |
| x1 |
| 2 |
| x12 |
| 4 |
| x2 |
| 2 |
| x22 |
| 4 |
联立
|
|
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
联立
|
∴x1+x2=4k,x1x2=-4,∴点M(2k,-1).
把点M的坐标代入圆C2的方程得4k2+1=8,解得k=±
| ||
| 2 |
∴点M(±
| 7 |
(Ⅱ)是直线l的方程为y=kx+
| p |
| 2 |
对x2=2py求导得y′=
| x |
| p |
∴切线MA,MB的方程分别为y=
| x1 |
| p |
| x12 |
| 2p |
| x2 |
| p |
| x22 |
| 2p |
| x1+x2 |
| 2 |
| x1x2 |
| 2p |
由
|
∴点M(pk,-
| p |
| 2 |
| p2 |
| 4 |
又弦长|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
| (1+k2)(4p2k2+4p2) |
点M到直线l的距离d=
|pk2-(-
| ||||
|
| k2+1 |
∴S△MAB=
| 1 |
| 2 |
| k2+1 |
| k2+1 |
由(*)得p2=
| 32 |
| 4k2+1 |
32(1+k2)
| ||
| 4k2+1 |
令1+k2=t≥1,则S△MAB=
32t
| ||
| 4t-3 |
16
| ||
| (4t-3)2 |
∵在区间[1,
| 9 |
| 4 |
∵在区间(
| 9 |
| 4 |
∴当t=
| 9 |
| 4 |
| 5 |
| 4 |
| 16 |
| 3 |
此时抛物线的方程为x2=
8
| ||
| 3 |
点评:熟练掌握直线与圆锥曲线的相交、相切问题的解题模式、弦长公式、点到直线的距离公式、三角形的面积公式、利用导数求斜率及研究函数的单调性、极值、最值等是解题的关键.

练习册系列答案
相关题目
 与抛物线
与抛物线 和圆
和圆 都相切,F是C1的焦点.
都相切,F是C1的焦点. 与抛物线
与抛物线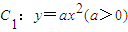 和圆
和圆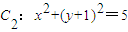 都相切,F是C1的焦点.
都相切,F是C1的焦点.