题目内容
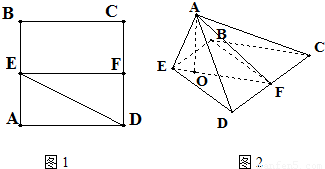
已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.(1)证明:BF∥平面ADE;
(2)证明:AE⊥平面ACD;
(3)求三棱锥F-ABC的体积.
【答案】分析:(1)由BE∥FD,BE=FD,知四边形BEDF为平行四边形,由此能够证明BF∥平面ADE.
(2)由AO⊥面BCDE,知AO⊥CD,由CD⊥EF,知CD⊥EF,由此能够证明AE⊥平面ACD.
(3)由BC=2,CF=1,知 =1,由AE⊥面ACD,知AE⊥AF,由EF=2,AE=1,知AF=
=1,由AE⊥面ACD,知AE⊥AF,由EF=2,AE=1,知AF= ,AD=
,AD= ,由此能求出三棱锥F-ABC的体积.
,由此能求出三棱锥F-ABC的体积.
解答:(1)证明:∵BE∥FD,BE=FD,
∴四边形BEDF为平行四边形,
∴ED∥BF,
∵ED?平面ADE,BF?平面ADE,
∴BF∥平面ADE.
(2)证明:∵AO⊥面BCDE,∴AO⊥CD,
又∵CD⊥EF,AO∩EF=O,
∴CD⊥EF,
∴CD⊥AE,
又∵AE⊥AD,AD∩CD=D,
∴AE⊥平面ACD.
(3)解:∵BC=2,CF=1,
∴ =1,
=1,
由(2)知:AE⊥面ACD,
∴AE⊥AF,
又∵EF=2,AE=1,
∴AF= ,
,
∴AD= =
= ,
,
∴VF-ABC=VA-BCF= =
= .
.
点评:本题考查直线与平面平行、直线与平面垂直的证明,考查三棱锥的体积的求法.解题时要注意合理地化立体问题为平面问题,注意空间思维能力的培养.
(2)由AO⊥面BCDE,知AO⊥CD,由CD⊥EF,知CD⊥EF,由此能够证明AE⊥平面ACD.
(3)由BC=2,CF=1,知
 =1,由AE⊥面ACD,知AE⊥AF,由EF=2,AE=1,知AF=
=1,由AE⊥面ACD,知AE⊥AF,由EF=2,AE=1,知AF= ,AD=
,AD= ,由此能求出三棱锥F-ABC的体积.
,由此能求出三棱锥F-ABC的体积.解答:(1)证明:∵BE∥FD,BE=FD,
∴四边形BEDF为平行四边形,
∴ED∥BF,
∵ED?平面ADE,BF?平面ADE,
∴BF∥平面ADE.
(2)证明:∵AO⊥面BCDE,∴AO⊥CD,
又∵CD⊥EF,AO∩EF=O,
∴CD⊥EF,
∴CD⊥AE,
又∵AE⊥AD,AD∩CD=D,
∴AE⊥平面ACD.
(3)解:∵BC=2,CF=1,
∴
 =1,
=1,由(2)知:AE⊥面ACD,
∴AE⊥AF,
又∵EF=2,AE=1,
∴AF=
 ,
,∴AD=
 =
= ,
,∴VF-ABC=VA-BCF=
 =
= .
.点评:本题考查直线与平面平行、直线与平面垂直的证明,考查三棱锥的体积的求法.解题时要注意合理地化立体问题为平面问题,注意空间思维能力的培养.

练习册系列答案
相关题目
 已知边长为
已知边长为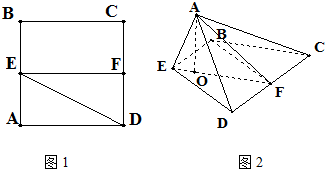 已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.
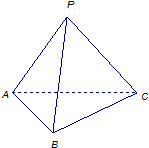
已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上. (2012•门头沟区一模)已知边长为2的正方形ABCD所在平面外有一点P,PA⊥平面ABCD,且PA=2,E是PC上的一点.
(2012•门头沟区一模)已知边长为2的正方形ABCD所在平面外有一点P,PA⊥平面ABCD,且PA=2,E是PC上的一点.