题目内容
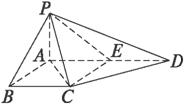
 如图四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,AB=2,PC与平面ABCD成45°角,E、F分别为PA、PB的中点.
如图四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,AB=2,PC与平面ABCD成45°角,E、F分别为PA、PB的中点.(1)求异面直线DE与AF所成角的大小;
(2)设M是PC上的动点,试问当M在何处时,才能使AM⊥平面PBD,证明你的结论.
分析:(1)取PF的中点G,连接EG,则EG∥AF,连接DG,则∠GED即为所求的角(或补角),在△DEG中由余弦定理可求
(2)建立如图所示的空间直角坐标系,设M(x,y,z),由题意可得
=(2,-2,-2
),
=(0,-2, -2
),设
=λ
=(2λ,-2λ,-2
λ)=(x,y,z-2
)可求M,由AM⊥平面PBD可得AM⊥PD即
•
=0,代入可求λ,即确定M在PC的位置
(2)建立如图所示的空间直角坐标系,设M(x,y,z),由题意可得
| PC |
| 2 |
| PD |
| 2 |
| PM |
| PC |
| 2 |
| 2 |
| AM |
| PD |
解答:解:(1)取PF的中点G,连接EG,则EG∥AF,连接DG,则∠GED即为所求的角(或补角)
∵PA⊥面ABCD
∴∠PCA即为直线PC与平面ABCD成的角则∠PCA=45°
∵AB=2
∴PA=AC=
AB=2
,PC=4,PB=2
在Rt△PAB中,由F为PB的中点可知,AF=
PB=
,∴EG=
AF=
,
在Rt△PAD中,由E为PA的中点可知,DE=
=
在△PDB中,由余弦定理可得,
=
即
=
∴DG=
△EDG中,由余弦定理可得,COS∠DEG=
=
=-
∴异面直线DE与AF所成角为arccos

(2)当M为PC的三分点,即
=
时,满足AM⊥平面PBD
证明如下:建立如图所示的空间直角坐标系,设M(x,y,z)
则可得D(0,-2,0),P(0,0,,2
),B(2,0,0),A(0,0,0),C(2,-2,0)
∴
=(2,-2,-2
),
=(0,-2, -2
)
设
=λ
=(2λ,-2λ,-2
λ)=(x,y,z-2
)
∴M(2λ,-2λ,2
-2
λ),即
=(2λ,-2λ,2
-2
λ),
∵AM⊥平面PBD
∴AM⊥PD即
•
=4λ-2
(2
-2
λ)=0
∴12λ-8-0
∴λ=
即
=

∵PA⊥面ABCD
∴∠PCA即为直线PC与平面ABCD成的角则∠PCA=45°
∵AB=2
∴PA=AC=
| 2 |
| 2 |
| 3 |
在Rt△PAB中,由F为PB的中点可知,AF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
在Rt△PAD中,由E为PA的中点可知,DE=
| AD2+AE2 |
| 6 |
在△PDB中,由余弦定理可得,
| PD2+PB2-BD2 |
| 2PB•PD |
| PD2+PG2-DG2 |
| 2PD•PG |
即
| 12+12-8 | ||||
2×2
|
12+
| ||||||
2×2
|
∴DG=
| ||
| 2 |
△EDG中,由余弦定理可得,COS∠DEG=
| DE2+EG2-DG2 |
| 2DE•EG |
6+
| ||||||
2
|
| ||
| 3 |
∴异面直线DE与AF所成角为arccos
| ||
| 3 |

(2)当M为PC的三分点,即
| PM |
| 2 |
| 3 |
| PC |
证明如下:建立如图所示的空间直角坐标系,设M(x,y,z)
则可得D(0,-2,0),P(0,0,,2
| 2 |
∴
| PC |
| 2 |
| PD |
| 2 |
设
| PM |
| PC |
| 2 |
| 2 |
∴M(2λ,-2λ,2
| 2 |
| 2 |
| AM |
| 2 |
| 2 |
∵AM⊥平面PBD
∴AM⊥PD即
| AM |
| PD |
| 2 |
| 2 |
| 2 |
∴12λ-8-0
∴λ=
| 2 |
| 3 |
即
| PM |
| 2 |
| 3 |
| PC |

点评:在立体几何中线面,线线的平行与垂直关系是经常考查的问题,以及线面角,线线角在高考中占分比较重.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
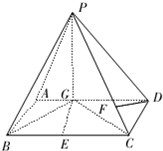 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且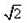 ,F是BC的中点.
,F是BC的中点.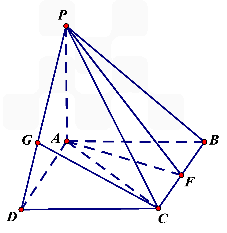
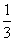 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.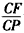 的值。
的值。 
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.