题目内容
双曲线
-
=1的两个焦点为F1、F2，点P在双曲线上.若PF1⊥PF2，则点P到x轴的距离为______________.
思路解析：P点到x轴的距离即为P点的纵坐标的绝对值，结合PF1⊥PF2，及P为双曲线上的点求得P的坐标. 解法一：如图所示，焦点F1（-5，0），F2（5，0）.设点P的坐标为（x0,y0），又PF1⊥PF2,得|PF1|2+|PF2|2=|F1F2|2，故有 解得|y0|= 解法二：依题设得双曲线的焦点为F1（-5，0），F2（5，0）.设P（x0,y0），则PF1⊥PF2. ∴ 代入双曲线方程,得 ∴y02=（ 解法三：依题设,得F1（-5，0），F2（5，0）. 设P（x0,y0），则 由PF1⊥PF2，得|OP|= 由①②得方程组
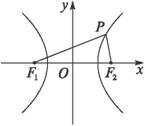
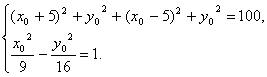
.故填
.
·
=-1,化简得x02=25-y02.
-（
+
）y02=1.
）2.∴P到x轴距离为|y0|=
.
=1.①
|F1F2|=5， ∴有x02+y02=25.②
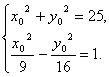解得y02=（
）2.∴P到x轴的距离为
.
练习册系列答案
金钥匙期末冲刺100分系列答案
初中英语听力训练苏州大学出版社系列答案
教与学中考必备系列答案
培优好卷系列答案
期末在线系列答案
全程评价与自测系列答案
小学升初中试卷精编系列答案
红对勾课堂巧练系列答案
相关题目
＝1(a＞0，b＞0)上一点P(x0，y0)与两个焦点F1(－c，0)、F2(c，0)间的距离，则r1＝________；r2＝________．(双曲线的焦半径公式)
＝1(a＞0，b＞0)上一点P(x0，y0)与两个焦点F1(－c，0)、F2(c，0)间的距离，则r1＝________，r2＝________．(双曲线的焦半径公式)
的方程为 
，双曲线
的左、右焦
与双曲线C2恒有两个不同的交点A和B，求
的范围。