Question

【题目】在等比数列{an}中，前7项和S7=16，又a12+a22+…+a72=128，则a1﹣a2+a3﹣a4+a5﹣a6+a7=（ ）
A.8
B.
C.6
D.

Answer 1

【答案】A
【解析】解答：∵S7= 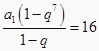， ∴a12+a22+…+a72= 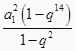= =128，
即
则a1﹣a2+a3﹣a4+a5﹣a6+a7=（a1﹣a2）+（a3﹣a4）+（a5﹣a6）+a7
=a1（1﹣q）+a1q2（1﹣q）+a1q4（1﹣q）+a1q6= +a1q6
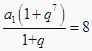= ；故选A
分析：把已知的前7项和S7=16利用等比数列的求和公式化简，由数列{an2}是首项为a1 ， 公比为q2的等比数列，故利用等比数列的求和公式化简a12+a22+…+a72=128，变形后把第一个等式的化简结果代入求出 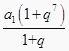的值，最后把所求式子先利用等比数列的通项公式化简，把前六项两两结合后，发现前三项为等比数列，故用等比数列的求和公式化简，与最后一项合并后，将求出 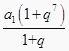的值代入即可求出值．