题目内容
 已知函数
已知函数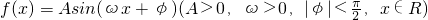 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(1)求函数f(x)的解析式;
(2)当x∈[-6,2]时,求函数g(x)=f(x)+f(x+2)的单调递增区间.
解:(1)由图象知A=2, ,
,
∴T=8,
∴ ,得
,得 .…(3分)
.…(3分)
又图象经过点(-1,0),
∴ .
.
∵ ,
,
∴由 ,得
,得 ,故函数f(x)的解析式为
,故函数f(x)的解析式为 .…(6分)
.…(6分)

(2)∵g(x)=f(x)+f(x+2)
=
=
=
= …(9分)
…(9分)
由 ,得8k-4≤x≤8k(k∈Z).
,得8k-4≤x≤8k(k∈Z).
又x∈[-6,2],故g(x)的单调递增区间为[-4,0].…(12分)
分析:(1)由图象知A=2,由 可求得ω,又图象经过点(-1,0),可求得φ;
可求得ω,又图象经过点(-1,0),可求得φ;
(2)由f(x)=2sin( x+
x+ ),可得f(x+2)=2cos(
),可得f(x+2)=2cos( x+
x+ ),于是g(x)=f(x)+f(x+2)=
),于是g(x)=f(x)+f(x+2)= ,从而可求g(x)的单调递增区间.
,从而可求g(x)的单调递增区间.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,A、ω、φ的确定是关键,化简g(x)= 是难点.属于中档题.
是难点.属于中档题.
 ,
,∴T=8,
∴
 ,得
,得 .…(3分)
.…(3分)又图象经过点(-1,0),
∴
 .
.∵
 ,
,∴由
 ,得
,得 ,故函数f(x)的解析式为
,故函数f(x)的解析式为 .…(6分)
.…(6分)
(2)∵g(x)=f(x)+f(x+2)
=

=

=

=
 …(9分)
…(9分)由
 ,得8k-4≤x≤8k(k∈Z).
,得8k-4≤x≤8k(k∈Z).又x∈[-6,2],故g(x)的单调递增区间为[-4,0].…(12分)
分析:(1)由图象知A=2,由
 可求得ω,又图象经过点(-1,0),可求得φ;
可求得ω,又图象经过点(-1,0),可求得φ;(2)由f(x)=2sin(
 x+
x+ ),可得f(x+2)=2cos(
),可得f(x+2)=2cos( x+
x+ ),于是g(x)=f(x)+f(x+2)=
),于是g(x)=f(x)+f(x+2)= ,从而可求g(x)的单调递增区间.
,从而可求g(x)的单调递增区间.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,A、ω、φ的确定是关键,化简g(x)=
 是难点.属于中档题.
是难点.属于中档题. 
练习册系列答案
相关题目
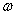 x(A>0,
x(A>0,
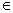 [0,4]的图象,且图象的最高点为S(3,2
[0,4]的图象,且图象的最高点为S(3,2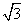 );赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定
);赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定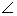 MNP=120
MNP=120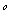
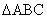 中
中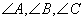 所对的边分别为
所对的边分别为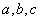 ;满足:
;满足: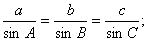
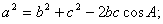
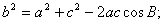
 )
)