题目内容
在△ABC中,已知tan
=sinC,则( )
| A+B |
| 2 |
分析:由于tan
=tan
=cot
,结合tan
=sinC可求得cosC=0,从而可从选项中得到答案.
| A+B |
| 2 |
| π-C |
| 2 |
| C |
| 2 |
| A+B |
| 2 |
解答:解:∵tan
=tan
=cot
=
=sinC=2sin
cos
,cos
≠0,
∴1-2sin2
=0,即cosC=0,又0<C<π,
∴C=
.
∴tanAcotB=tanA•tanA,不一定为1,故A不正确;
sinA•sinB=sinA•cosA=
sin2A ≤
故排除B;
sin2A+cos2B=sin2A+sin2A不一定为1,排除C,
cos2A+cos2B=cos2A+sin2A=1=sin2C,D正确;
故选D.
| A+B |
| 2 |
| π-C |
| 2 |
| C |
| 2 |
cos
| ||
sin
|
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
∴1-2sin2
| C |
| 2 |
∴C=
| π |
| 2 |
∴tanAcotB=tanA•tanA,不一定为1,故A不正确;
sinA•sinB=sinA•cosA=
| 1 |
| 2 |
| 1 |
| 2 |
sin2A+cos2B=sin2A+sin2A不一定为1,排除C,
cos2A+cos2B=cos2A+sin2A=1=sin2C,D正确;
故选D.
点评:本题考查拌脚的三角函数,着重考查是诱导公式的熟练应用,关键在于确定C=
,属于中档题.
| π |
| 2 |

练习册系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.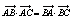 .
. |=|
|=| |;
|; ,求|
,求| -t
-t