题目内容
设函数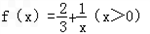
，数列{an}满足
．
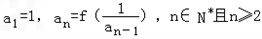（1）求数列{an}的通项公式；
（2）对n∈N*，设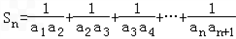
，若
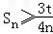恒成立，求实数t的取值范围．
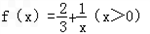，数列{an}满足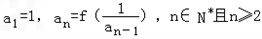．（1）求数列{an}的通项公式；
（2）对n∈N*，设
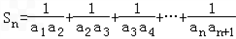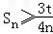，若恒成立，求实数t的取值范围．解：（I）由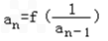 
可得an﹣an﹣1=
，n≥2，
故数列{an}为等差数列，又a1=1，它的通项公式an=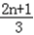
．
（II）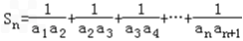
，
由（I）得an=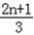
．an+1= 
．
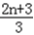∴anan+1=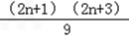
，
∴
= 
，
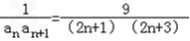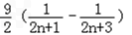∴Sn=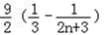
=
，
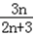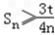
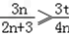
t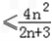 
，
令g（n）=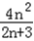
， g（n）=
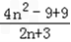=2n+3+ 
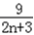﹣6，
由于2n+3≥5，故g（n）的最小值为
，
∴t
，
∴实数t的取值范围（﹣∞，
]．
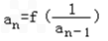可得an﹣an﹣1= ，n≥2，故数列{an}为等差数列，又a1=1，它的通项公式an=
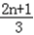．（II）
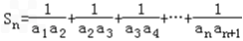，由（I）得an=
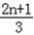．an+1= 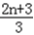． ∴anan+1=
，∴
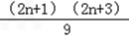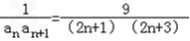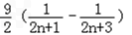= ，∴Sn=
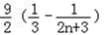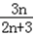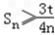
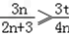
= ， t 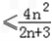，令g（n）=
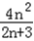， g（n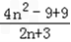）= =2n+3+ 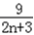﹣6，由于2n+3≥5，故g（n）的最小值为
， ∴t
， ∴实数t的取值范围（﹣∞，
]．
练习册系列答案
相关题目
，数列{an}满足
，试比较 Sn与
的大小，并加以证明．
，数列{an}满足
，试比较 Sn与
的大小，并加以证明．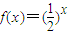
，数列{an} 满足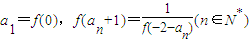 
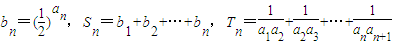，求 Sn与 Tn．
，数列{an}满足
．
，这些项能够构成以a1为首项，q（0＜q＜5，q∈N*）为公比的等比数列
，k∈N*．若存在，写出nk关于k的表达式；若不存在，说明理由．