题目内容
如图是足球场的部分示意图,假设球门的宽AB=7m,A到边线的距离AC=30m.现距离边线5m处的一名运动员P沿着边线方向向底线运球,他观察球门的角∠APB称为视角.设P到底线的距离为PD=xm,tan∠APB记为y.
(1)试将y表示成x的函数;
(2)求当P离底线多少m时,该球员观察球门的视角最大?(结果保留根式)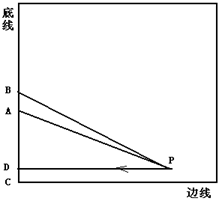
(1)试将y表示成x的函数;
(2)求当P离底线多少m时,该球员观察球门的视角最大?(结果保留根式)

(1)由题意,AD=25m,BD=32m,∠APB=∠DPB-∠DPA
∴y=tan∠APB=tan(∠DPB-∠DPA)=
=
∴y=
(x>0);
(2)y=
≤
=
,当且仅当x=20
m时,取等号
∴x=20
m时,y=tan∠APB取得最大值
∵∠APB∈(0,
)
∴x=20
m时,∠APB取得最大值.
∴y=tan∠APB=tan(∠DPB-∠DPA)=
| tan∠DPB-tan∠DPA |
| 1+tan∠DPBtan∠DPA |
| ||||
1+
|
∴y=
| 7x |
| x2+800 |
(2)y=
| 7 | ||
x+
|
| 7 | ||
2
|
7
| ||
| 80 |
| 2 |
∴x=20
| 2 |
∵∠APB∈(0,
| π |
| 2 |
∴x=20
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是足球场的部分示意图,假设球门的宽AB=7m,A到边线的距离AC=30m.现距离边线5m处的一名运动员P沿着边线方向向底线运球,他观察球门的角∠APB称为视角.设P到底线的距离为PD=xm,tan∠APB记为y.
如图是足球场的部分示意图,假设球门的宽AB=7m,A到边线的距离AC=30m.现距离边线5m处的一名运动员P沿着边线方向向底线运球,他观察球门的角∠APB称为视角.设P到底线的距离为PD=xm,tan∠APB记为y.