题目内容
.如下图,已知在正方形ABCD中,有四个全等的直角三角形,设直角三角形的两条直角边的长为a、b,则正方形ABCD的面积为S1=__________,4个直角三角形面积的和为S2=__________,则S1__________S2(填“≥”“≤”或“=”).据此,我们就可得到一个不等式__________(用a、b的式子表示),并且当a__________b时,直角三角形变为__________时,S1=S2.

a2+b2 2ab ≥ a2+b2≥2ab = 等腰直角三角形
解析:
本题考查不等式a2+b2≥2ab的几何意义.
因为直角三角形的直角边长为a、b,
所以正方形的边长为![]() .而4个直角三角形的面积和为2ab,
.而4个直角三角形的面积和为2ab,
由图形可知a2+b2≥2ab.
当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有a2+b2=2ab.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
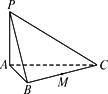
 侧棱
侧棱 的中点,过D作平面PAC的垂线,则该垂线与正方体表面的另一个交点Q(不同于D)的位置在________.
的中点,过D作平面PAC的垂线,则该垂线与正方体表面的另一个交点Q(不同于D)的位置在________.