Question

在长方体ABCD-A₁B₁C₁D₁中，AB=4，BC=2，CC₁=3，
（1）求点D₁到平面BDE的距离；
（2）求直线A₁B与平面BDE所成角的正弦值．

Answer 1

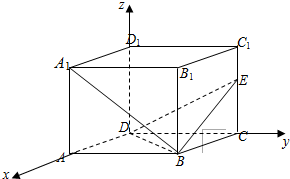解：（1）如图建立空间直角坐标系：
D（0，0，0），B（2，4，0），E（0，4，2），D₁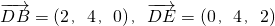（0，0，3），
∴，=（0，0，3）
设面DBE的法向量为，
由，
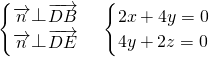令y=1，则x=-2，z=-2．
．
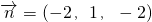
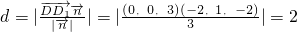（2）A₁（2，0，3），B（2，4，0），
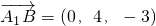
设 直线A₁B与平面BDE所成的角为θ．
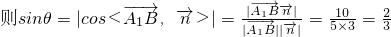所以直线A₁B与平面BDE所成角的正弦值为 ．
分析：（1）分别以DA，DC，DD₁所在直线为x轴，y轴，z轴建立空间直角坐标系，写出相关点的坐标，求出平面BDE的一个法向量，根据向量数量积的几何意义即可求得结果；
（2）要求直线A₁B与平面BDE所成角的正弦值，即求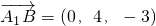与平面BDE的一个法向量夹角的余弦值的绝对值即可．
点评：本题考查利用空间直角坐标系求点到面的距离和直线与平面所成的角，准确写出坐标是解题的关键，考查运算能力，属中档题．